1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Tl5Zq
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
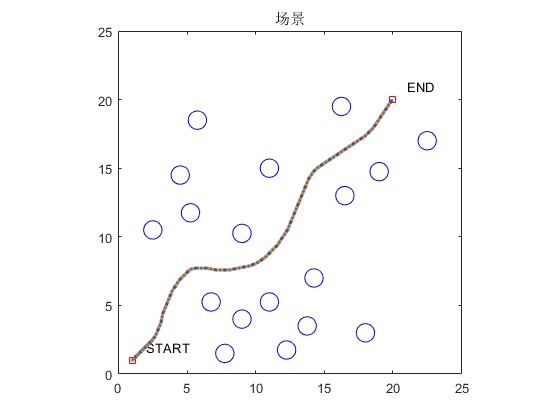
3.算法概述
在BP神经网络中,隐含层数量对神经网络的性能有着至关重要的影响,如果隐含层数量过多,会大大增加BP神经网络的内部结构的复杂度,从而降低学习效率,增加训练时间;如果隐含层数量过少,则无法精确获得训练输入数据和输出结果之间的内在规律,增加预测误差。因此,选择合适的隐含层个数具有十分重要的意义。由于隐含层个数的设置没有明确的理论可以计算,通常情况下,采用逐次分析的方法获得,即通过对不同隐含层所对应的神经网络进行预测误差的仿真分析,选择误差最小情况下所对应的隐含层个数。
4.部分源码
for time = 1:TIME
time
%计算四个输入
if time <= 3
x(:,time)= min(x(:,time),xmax);
x(:,time)= max(x(:,time),xmin);
Xs(time) = X_start;
Ys(time) = Y_start;
Theta = atan((Y_end-Y_start)/(X_end-X_start));
else
x(:,time)= min(x(:,time),xmax);
x(:,time)= max(x(:,time),xmin);
%计算alpha,机器人运动方向与目标方向之间的夹角
%计算alpha,机器人运动方向与目标方向之间的夹角
if X_end-Xs(time-1) == 0
tmps1 = inf;
else
tmps1 =(Y_end-Ys(time-1))/(X_end-Xs(time-1));
end
if Xs(time-1)-Xs(time-2) == 0
tmps2 = inf;
else
tmps2 =(Ys(time-1)-Ys(time-2))/(Xs(time-1)-Xs(time-2));
end
%目标方向 %运动方向
alpha = atan(tmps1) - atan(tmps2);
%先计算障碍物和机器人的距离,然后将这些距离划分为四类,dr,d,dl和反方向的,如果没有,那么认为距离为inf
dr = [];
dl = [];
d = [];
vdr = [];
vdl = [];
vd = [];
for kk = 1:N
%计算距离,障碍物和小车当前位置的间距
dist(kk) = sqrt((xobstacle(kk)-Xs(time-1))^2 + (yobstacle(kk)-Ys(time-1))^2)-R(kk);
if xobstacle(kk)-Xs(time-1) == 0
vdist(kk) = 1;
else
vdist(kk) = sign((yobstacle(kk)-Ys(time-1))/(xobstacle(kk)-Xs(time-1)));
end
if dist(kk)>0
%计算各个距离和机器人运动方向的夹角
if xobstacle(kk)-Xs(time-1) == 0
tmps3 = inf;
else
tmps3 =(yobstacle(kk)-Ys(time-1))/(xobstacle(kk)-Xs(time-1));
end
Beta(kk) = (atan(tmps3))*180/pi;
%根据角度差,分析哪些是dr,d,dl和反方向
%说明这个障碍物在运动方向的右边
if Beta(kk) > 15 & Beta(kk) <= 75
dr = [dr,dist(kk)];
dl = dl;
d = d;
vdr = [vdr,vdist(kk)];
vdl = vdl;
vd = vd;
end
%说明这个障碍物在运动方向的左边边
if Beta(kk) < -15 & Beta(kk) >= -75
dr = dr;
dl = [dl,dist(kk)];
d = d;
vdr = vdr;
vdl = [vdl,vdist(kk)];
vd = vd;
end
%说明这个障碍物在运动方向的前边
if Beta(kk) <= 15 & Beta(kk) >= -15
dr = dr;
dl = dl;
d = [d,dist(kk)];
vdr = vdr;
vdl = vdl;
vd = [vd,vdist(kk)];
end
end
end
for m=1:Ns
xs(:,m) = [x(1,time-1) + Sense_radius*cos(Jd(m,1));
x(2,time-1) + Sense_radius*sin(Jd(m,1))];
G1(m,1) = func_obstacle(xs(:,m),xobstacle,yobstacle);
G2(m,1) = func_goal(xs(:,m),Pend);
G3(m,1) = G1(m,1) + G2(m,1);
end
[val,bestone]=min(G3);
%如果某个方向有多个障碍物,那么选择最近的那个
%如果某个方向的距离集合为空集合,那么说明这个方向的障碍物为无穷远,直接赋值一个较大值
dr_in = min(dr);
if isempty(dr) == 1
dr_in = 1e20;
end
d_in = min(d);
if isempty(d) == 1
d_in = 1e20;
end
dl_in = min(dl);
if isempty(dl) == 1
dl_in = 1e20;
end
%代入到BP神经网络的四个变量
%调用BP神经网络的模型
YOUT = func_nn_test(dr_in,d_in,dl_in,alpha,net);
%计算速度和方向
DELTA_Theta = YOUT/10;
V = YOUT;
%更新小车坐标
x(:,time) =[x(1,time-1)+lambda*cos(Jd(bestone,1));
x(2,time-1)+lambda*sin(Jd(bestone,1))];
Deltalambda = V;
Deltatheta = DELTA_Theta;
%更新小车坐标
x(:,time) =[x(1,time)+Deltalambda*cos(Jd(bestone,1)+Deltatheta);
x(2,time)+Deltalambda*sin(Jd(bestone,1)+Deltatheta)];
%更新坐标
Xs(time) = x(1,time);
Ys(time) = x(2,time);
Tes = [Tes,Jd(bestone,1)+Deltatheta];
Vs = [Vs,Deltalambda];
end
%画图
plot(x(1,time),x(2,time),'.')
hold on
drawnow;
if sqrt((Xs(time)-X_end)^2+(Ys(time)-Y_end)^2)<0.2
break;
end
end
05_048_m





































