1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Wmp1r
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览

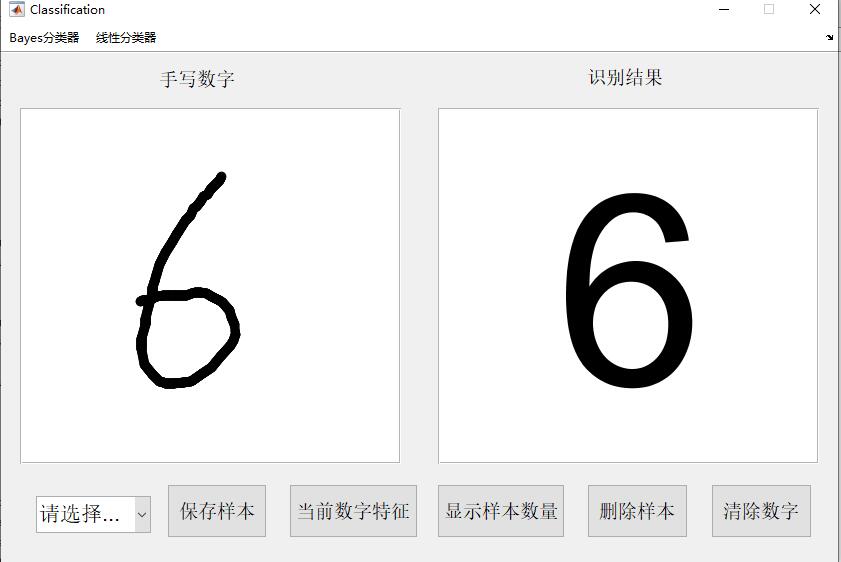
3.算法概述
贝叶斯判别规则是把某特征矢量(x) 落入某类集群的条件概率当成分类判别函数(概率判别函数),x落入某集群的条件概率最大的类为X的类别,这种判决规则就是贝叶斯判别规则。贝叶斯判别规则是以错分概率或风险最小为准则的判别规则。
判别函数,各个类别的判别区域确定后,可以用一些函数来表示和鉴别某个特征矢量属于哪个类别,这些函数就称为判别函数。这些函数不是集群在特征空间形状的数学描述,而是描述某一位置矢量属于某个类别的情况,如属于某个类别的条件概率,一般不同的类别都有各自不同的判别函数。
4.部分源码
function y=BayesLeastRisk(data)
clc;
load template pattern;
%将数字特征转化为0、1两个数值表示
for i=1:10
for j=1:25
for k=1:pattern(1,i).num
if pattern(1,i).feature(j,k)>0.1
pattern(1,i).feature(j,k)=1;
else
pattern(1,i).feature(j,k)=0;
end
end
end
end
[pc_template,pc_data]=pcapro(data); %主成分分析
temp=0;
for i=1:10
pattern(1,i).feature=pc_template(:,temp+1:temp+pattern(1,i).num);
temp=temp+pattern(1,i).num;
end
%求协方差矩阵、协方差矩阵的逆矩阵、协方差矩阵的行列式
s_cov=[];
s_inv=[];
s_det=[];
for i=1:10
s_cov(i).data=cov(pattern(1,i).feature');
s_inv(i).data=inv(s_cov(i).data);
s_det(i)=det(s_cov(i).data);
end
%求先验概率
sum=0;
pw=[]; %P(wi)---先验概率
for i=1:10
sum=sum+pattern(1,i).num;
end
for i=1:10
pw(i)=pattern(1,i).num/sum;
end
%求判别函数
h=[]; %h()---差别函数
mean_data=[]; %mean_data---每类样品特征向量的均值
for i=1:10
mean_data(i).data=mean(pattern(1,i).feature')';
end
%判别函数
for i=1:10
h(i)=(pc_data-mean_data(i).data)'*s_inv(i).data*(pc_data-mean_data(i).data)...
*(-0.5)+log(pw(i))+log(abs(s_det(i)))*(-0.5);
end
%求每一类的损失
%---------loss为损失矩阵,大小为10x10---------------------------------------
loss=ones(10)-diag(diag(ones(10))); %diag(ones(10))---取对角线元素,diag(diag(ones(10)))---构建以上面取得的对角线元素为新矩阵的对角线元素,其余元素为0的新的对角线元素。
risk=0;
m=[];
for i=1:10
m=loss(i,:); %根据每一类损失的公式,第i类的损失等损失矩阵的第i行与判别函数的列向量相乘
risk(i)=m*h';
end
[minval minpos]=min(risk);
y=minpos-1;
end
A253





































