1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5iUl5lv
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
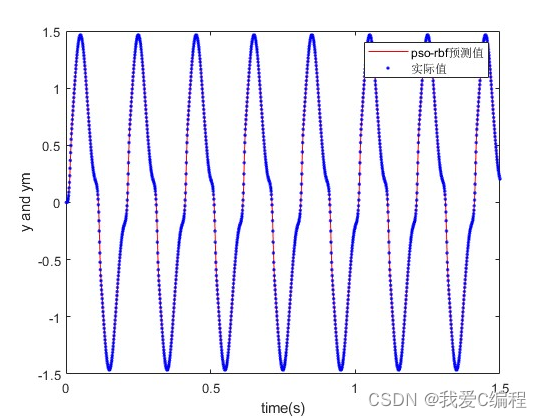
2.部分仿真图预览
3.算法概述
径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也可以是到任意一点c的距离,c点称为中心点。任意满足上述特性的函数,都可以叫做径向基函数。一般使用欧氏距离计算距离中心点的距离(欧式径向基函数)。最常用的径向基函数是高斯核函数。RBF神经网络只有三层,即输入层、隐藏层、输出层。RBF网络的基本思想是:用RBF作为隐单元的“基”构成隐含层空间,这样就可以将输入矢量直接映射到隐空间,而不需要通过权连接。当RBF的中心点确定以后,这种映射关系也就确定了。而隐含层空间到输出空间的映射是线性的,即网络的输出是隐单元输出的线性加权和,此处的权即为网络可调参数。其中,隐含层的作用是把向量从低维度的p映射到高维度的h,这样低维度线性不可分的情况到高维度就可以变得线性可分了,主要就是核函数的思想。
4.部分源码
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
V = 0.1*rands(m,n);
BsJ = 0;
%根据初始化的种群计算个体好坏,找出群体最优和个体最优
for s = 1:m
indivi = pop(s,:);
[indivi,BsJ] = func_obj(indivi,BsJ);
Error(s) = BsJ;
end
[OderEr,IndexEr] = sort(Error);
Error;
Errorleast = OderEr(1);
for i = 1:m
if Errorleast == Error(i)
gbest = pop(i,:);
break;
end
end
ibest = pop;
for kg = 1:G
kg
for s = 1:m;
%个体有4%的变异概率
for j = 1:n
for i = 1:m
if rand(1)<0.04
pop(i,j) = rands(1);
end
end
end
%r1,r2为粒子群算法参数
r1 = rand(1);
r2 = rand(1);
%个体和速度更新
V(s,:) = w*V(s,:) + c1*r1*(ibest(s,:)-pop(s,:)) + c2*r2*(gbest-pop(s,:));
pop(s,:) = pop(s,:) + 0.3*V(s,:);
for j = 1:3
if pop(s,j) < MinX(j)
pop(s,j) = MinX(j);
end
if pop(s,j) > MaxX(j)
pop(s,j) = MaxX(j);
end
end
for j = 4:9
if pop(s,j) < MinX(j)
pop(s,j) = MinX(j);
end
if pop(s,j) > MaxX(j)
pop(s,j) = MaxX(j);
end
end
for j = 10:12
if pop(s,j) < MinX(j)
pop(s,j) = MinX(j);
end
if pop(s,j) > MaxX(j)
pop(s,j) = MaxX(j);
end
end
%求更新后的每个个体适应度值
[pop(s,:),BsJ] = func_obj(pop(s,:),BsJ);
error(s) = BsJ;
%根据适应度值对个体最优和群体最优进行更新
if error(s)<Error(s)
ibest(s,:) = pop(s,:);
Error(s) = error(s);
end
if error(s)<Errorleast
gbest = pop(s,:);
Errorleast = error(s);
end
end
Best(kg) = Errorleast;
end
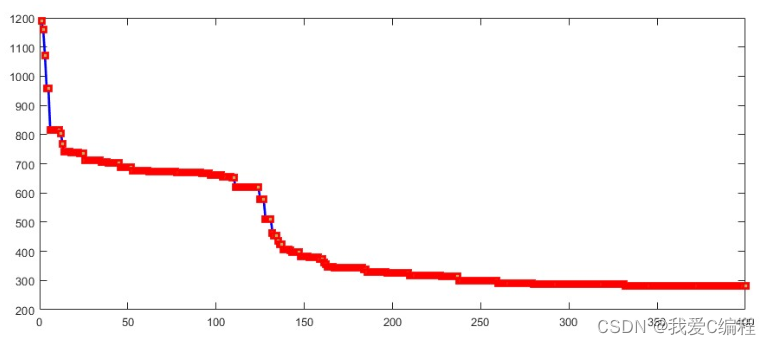
plot(Best,'-bs',...
'LineWidth',2,...
'MarkerSize',6,...
'MarkerEdgeColor','r',...
'MarkerFaceColor',[0.7,0.7,0.4]);
save net.mat gbest;
A286