1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qZmp5q
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
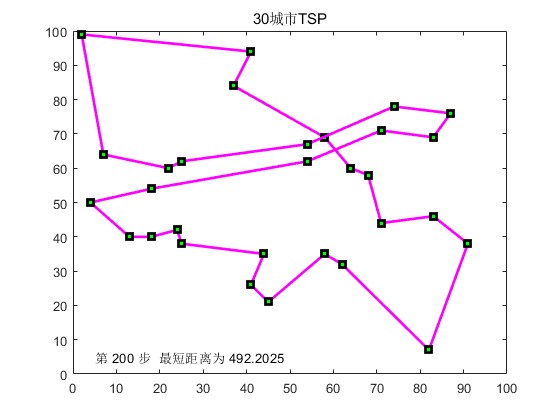
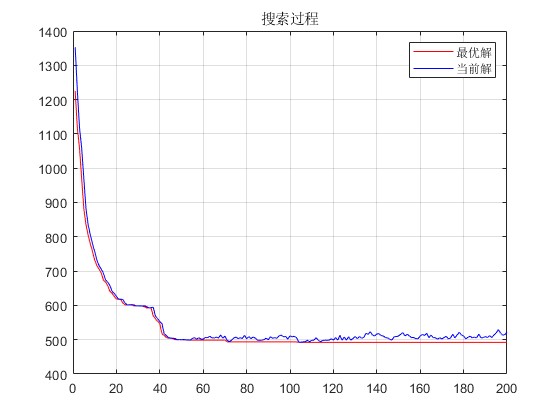
3.算法概述
禁忌搜索算法在初始化时,在搜索空间中随机生成初始解I、禁忌表H 置空,将当前解I记录为历史最优解s,进入迭代搜索过程。 对于每次迭代,从当前解I开始,在当前禁忌表h的限制下,构造解I的邻域A,从a中选出适应值最好的解j替换解I,同时http://www 否则,s保持不变,即使解I暂时变差,也有利于通过扩大搜索空间来摆脱局部最优。 在获得新的当前解I之后,该算法返回开始迭代,并且在找到最佳解或已经执行更新(例如,一定的迭代次数)时结束该算法。
禁忌搜索算法的一般流程如下:
(1)初始化TS算法的参数,按照准则生成问题的初始解,生成0禁忌表;
(2)判断是否满足终止条件,若是,则结束算法,输出结果
(3)根据算法的特性生成领域解,并从中选择合适规模大小的候选解;
(4)判断候选解中的最优解Next是否满足特赦准则,若满足特赦准则,则用Next替代当前最优解Before,并更新禁忌表,令Next对应的禁忌对象的禁忌长度为最长,即禁忌时间最长;若不满足特赦准则,进行(4)步骤;
(5)判断候选解中禁忌状态情况,找出候选解中处于“非禁忌”状态的禁忌对象,并把该禁忌对象对应的解赋给当前最优解,同时设置该禁忌对象的禁忌时间为最长;
(6)转(2);
4.部分源码
.......................
Tlist=zeros(CityNum);%禁忌表(tabu list)
cl=100;%保留前cl个最好候选解
bsf=Inf;
tl=50; %禁忌长度(tabu length)
l1=200;%候选解(candidate),不大于n*(n-1)/2(全部领域解个数)
S0=randperm(CityNum);
S=S0;
BSF=S0;
Si=zeros(l1,CityNum);
StopL=200; %终止步数
p=1;
clf;
figure(1);
while (p<StopL+1)
if l1>CityNum*(CityNum)/2
disp('候选解个数,不大于n*(n-1)/2(全部领域解个数)! 系统自动退出!');
l1=(CityNum*(CityNum)/2)^.5;
break;
end
ArrS(p)=CalDist(dislist,S);
i=1;
A=zeros(l1,2);
while i<=l1
M=CityNum*rand(1,2);
M=ceil(M);
if M(1)~=M(2)
m1=max(M(1),M(2));m2=min(M(1),M(2));
A(i,1)=m1;A(i,2)=m2;
if i==1
isdel=0;
else
for j=1:i-1
if A(i,1)==A(j,1)&&A(i,2)==A(j,2)
isdel=1;
break;
else
isdel=0;
end
end
end
if ~isdel
i=i+1;
else
i=i;
end
else
i=i;
end
end
for i=1:l1
Si(i,:)=S;
Si(i,[A(i,1),A(i,2)])=S([A(i,2),A(i,1)]);
CCL(i,1)=i;
CCL(i,2)=CalDist(dislist,Si(i,:));
CCL(i,3)=S(A(i,1));
CCL(i,4)=S(A(i,2));
end
[fs fin]=sort(CCL(:,2));
for i=1:cl
CL(i,:)=CCL(fin(i),:);
end
if CL(1,2)<bsf %藐视准则(aspiration criterion)
bsf=CL(1,2);
S=Si(CL(1,1),:);
BSF=S;
for m=1:CityNum
for n=1:CityNum
if Tlist(m,n)~=0
Tlist(m,n)=Tlist(m,n)-1;
end
end
end
Tlist(CL(1,3),CL(1,4))=tl;
else
for i=1:cl
if Tlist(CL(i,3),CL(i,4))==0
S=Si(CL(i,1),:);
for m=1:CityNum
for n=1:CityNum
if Tlist(m,n)~=0
Tlist(m,n)=Tlist(m,n)-1;
end
end
end
Tlist(CL(i,3),CL(i,4))=tl;
break;
end
end
end
Arrbsf(p)=bsf;
drawTSP(Clist,BSF,bsf,p,0);
p=p+1;
end
BestShortcut=BSF
theMinDistance=bsf
...................................
A136





































