1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJqXl5py
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
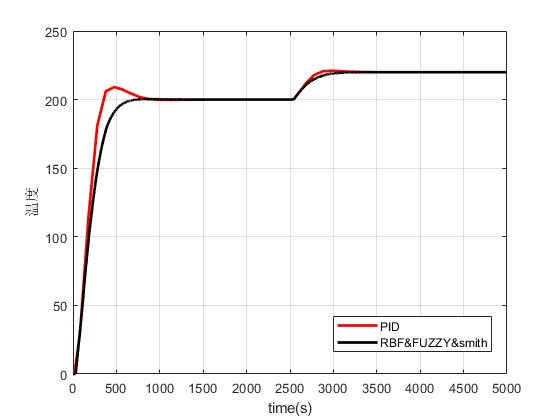
3.算法概述
Smith控制器是一种广泛应用于工业控制和自动化领域的经典控制算法。它通过引入一个延迟时间来补偿系统的时间滞后效应,从而提高系统的稳定性和控制性能。然而,传统的Smith控制器往往依赖于系统模型的精确性和参数的准确性,容易受到外部干扰和模型误差的影响,导致控制精度和鲁棒性较差。为了克服这些问题,一些研究者提出了基于RBF和模糊控制的Smith控制器。
4.部分源码
................................................................
str=[];
ts=[];
c1=12/3*[-5 -4 -3 -2 -1 0 1 2 3 4 5];
c2=16/3*[-5 -4 -3 -2 -1 0 1 2 3 4 5];
c=[c1;c2];
b=5;
function sys=mdlDerivatives(t,x,u)
global c b
y = u(1);
ut = u(2);
x1p= u(1);
x2p= u(2);
xp=[x1p x2p]';
yp=x2p;
ye=y-yp;
h=zeros(11,1);
for j=1:1:11
h(j)=exp(-norm(xp-c(:,j))^2/(2*b^2));
end
h_bar=x(23:1:33);
F1=1*eye(11);
F2=0.5*eye(11);
k1=0.001;k2=0.001;
W1=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)];
W2=[x(12) x(13) x(14) x(15) x(16) x(17) x(18) x(19) x(20) x(21) x(22)];
dW1=F1*h_bar*ye - k1*F1*abs(ye)*W1';
dW2=F2*h_bar*ye*ut - k2*F2*abs(ye)*W2';
for i=1:1:11
sys(i)=dW1(i);
sys(i+11)=dW2(i);
end
for i=23:1:33
sys(i)=h(i-22)-0.5*x(i);
end
function sys=mdlOutputs(t,x,u)
global c b
W1=[x(1) x(2) x(3) x(4) x(5) x(6) x(7) x(8) x(9) x(10) x(11)];
W2=[x(12) x(13) x(14) x(15) x(16) x(17) x(18) x(19) x(20) x(21) x(22)];
h_bar=x(23:1:33);
fxp=W1*h_bar;
gxp=W2*h_bar;
sys(1)=fxp;
sys(2)=gxp;
sys(3)=[fxp-gxp];
if sys(1)>=0.0025
sys(1)=0.0025;
end
if sys(1)<=-0.0025
sys(1)=-0.0025;
end
if sys(2)>=0.0025
sys(2)=0.0025;
end
if sys(2)<=-0.0025
sys(2)=-0.0205;
end
if sys(3)>=0.0025
sys(3)=0.0025;
end
if sys(3)<=-0.0025
sys(3)=-0.0025;
end
08_105_m





































