1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52YlJpt
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
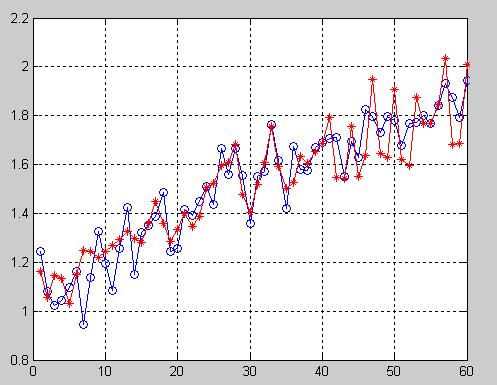
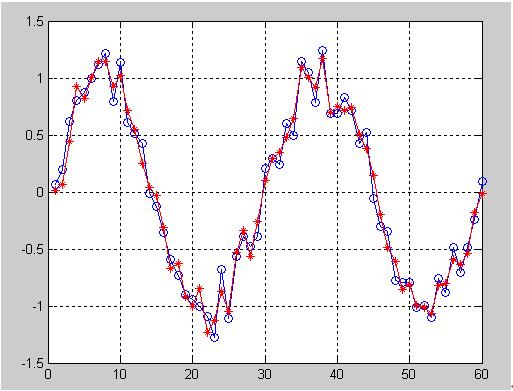
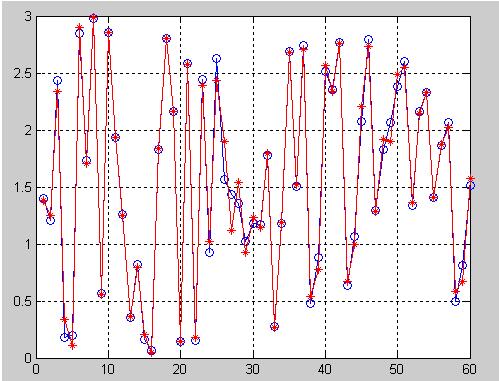
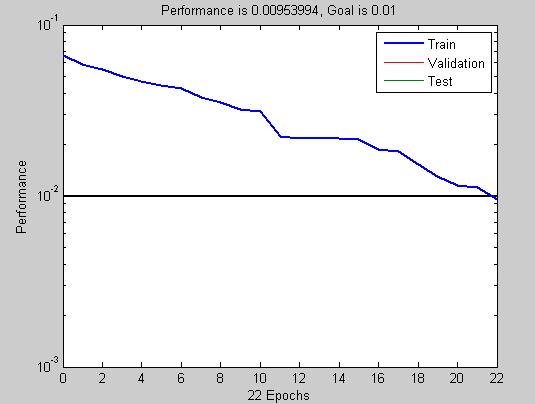
3.算法概述
径向基函数(RBF)方法。径向基函数是一个取值仅仅依赖于离原点距离的实值函数,也可以是到任意一点c的距离,c点称为中心点。任意满足上述特性的函数,都可以叫做径向基函数。一般使用欧氏距离计算距离中心点的距离(欧式径向基函数)。最常用的径向基函数是高斯核函数。RBF神经网络只有三层,即输入层、隐藏层、输出层。
4.部分源码
load data3.mat
%%
%选择100个数据作为输入
Data = data3(1:100);
%%
%选择20个训练数据
t11 = 1:10;
Train_data1 = Data(1:10);
t12 = 1:10;
spread = 1;
goal = 0.01;
df = 1;
mn = length(t11);
net = newrb(t11,Train_data1,goal,spread,mn,df);
yc1 = sim(net,t12);
%%
%选择70个训练数据
t21 = 1:60;
Train_data2 = Data(1:60);
t22 = 1:60;
spread = 1;
goal = 0.01;
df = 1;
mn = length(t21);
net = newrb(t22,Train_data2,goal,spread,mn,df);
yc2 = sim(net,t22);
figure;
plot(t21,Train_data2,'b-o');
hold on;
plot(t22,yc2,'r-*');
hold off;
grid on;
%%
%%对比计算结果
mser11 = func_mse(Train_data1);
mser12 = func_mse(yc1);
sder1 = func_sd(yc1);
sdrer1 = func_sdr(yc1,Train_data1);
coeff1 = func_pcc(yc1,Train_data1);
fprintf('Inputs Train data points MSE training MSE testing PCC SDR SD\n');
%%
%下面的程序是画图
cnt = 0;
for i = 10:2:60
i
cnt = cnt + 1;
t01 = 1:i;
Train_data0 = Data(1:i);
t02 = 1:i;
spread = 1;
goal = 0.01;
df = 1;
mn = length(t01);
net = newrb(t02,Train_data0,goal,spread,mn,df);
yc0 = sim(net,t02);
%%
%%对比计算结果
mser01(cnt) = func_mse(Train_data0);
mser02(cnt) = func_mse(yc0);
sder0(cnt) = func_sd(yc0);
sdrer0(cnt) = func_sdr(yc0,Train_data0);
end
05_008_m





































