1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJmVmJpp
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
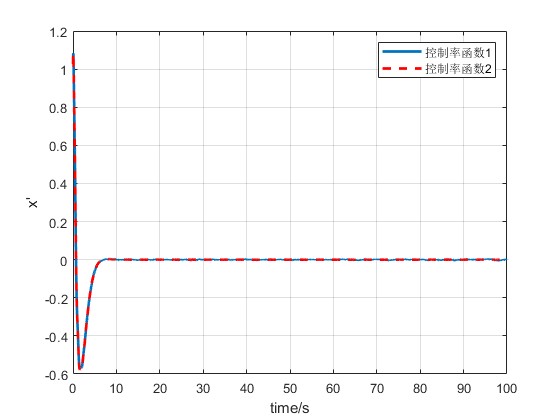
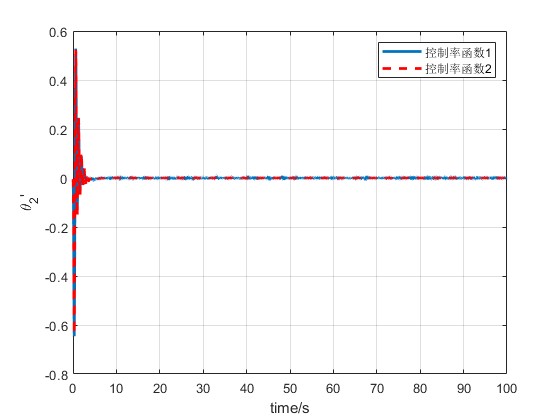
3.算法概述
在控制系统中,改变系统结构的思想最早是Wunch在1953年提出的。随后,各国学者在其研究成果的基础上提出了变结构控制系统的改进,并逐渐得到了一个全新控制系统的理论。而滑膜变控制理论(SMVSCS)属于变结构控制理论的主要研究方向之一[24,25]。滑膜变控制方法是首先是将控制系统的状态估计曲线转换到滑模超平面上,然后逐渐达到平衡点。通过滑膜变结构控制系统,可以原始高维度的控制系统降维成低维度系统,从而降低了整个系统的控制复杂度。
4.部分源码
...............................................................................
c = 1e-4;
if k==1
X_back2=0;
else
X_back2=X_back(k)-X_back(k-1);
end
s = c*X_back2;
y =-inv(C*B)*(C*A*s+5*s+0.05*sign(s));
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
X(k) = min(y);
u_0 = X(k);
x1_0 = x1(k);
x2_0 = x2(k);
x3_0 = x3(k);
x4_0 = x4(k);
x5_0 = x5(k);
x6_0 = x6(k);
end
x1a=x1;
x2a=x2;
x3a=x3;
x4a=x4;
x5a=x5;
x6a=x6;
A = [0,0 ,0 ,1,0,0;
0,0,0,0,1,0;
0,0,0,0,0,1;
0,0,0,0,0,0;
0,K12,K13,0,0,0;
0,K22,K23,0,0,0;];
B = [0;
0;
0;
1;
K17;
K27];
C = [0.4495,4.1930,-8.8675,0.8035,0.0151,-1.5196];
[F,G] = c2d(A,B,ts);
Q = diag([1 0 1 1 0 1]);
R = [1];
[K,p,e] = dlqr(F,G,Q,R);
F = F-G*K;
%初始条件
x1_0 = 1;
x2_0 = 0;
x3_0 = 0;
x4_0 = 1;
x5_0 = 0;
x6_0 = 0;
u_0 = 0;
for k=1:1:LEN
k
.................................................................
end
x1b=x1;
x2b=x2;
x3b=x3;
x4b=x4;
x5b=x5;
x6b=x6;
figure;
plot(time,x1a,'linewidth',2)
hold on
plot(time,x1b,'r--','linewidth',2)
xlabel('time/s');
ylabel('x');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x1a,'linewidth',2)
hold on
plot(time,x1b,'r--','linewidth',2)
xlabel('time/s');
ylabel('x');
grid on
legend('控制率函数1','控制率函数2');
axis([30,80,-6e-3,6e-3]);
figure;
plot(time,x2a,'linewidth',2)
hold on
plot(time,x2b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_1');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x2a,'linewidth',2)
hold on
plot(time,x2b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_1');
grid on
legend('控制率函数1','控制率函数2');
axis([20,90,-4e-3,4e-3]);
figure;
plot(time,x3a,'linewidth',2)
hold on
plot(time,x3b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_2');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x3a,'linewidth',2)
hold on
plot(time,x3b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_2');
grid on
legend('控制率函数1','控制率函数2');
axis([20,80,-1.5e-3,1.5e-3]);
figure;
plot(time,x4a,'linewidth',2)
hold on
plot(time,x4b,'r--','linewidth',2)
xlabel('time/s');
ylabel('x''');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x4a,'linewidth',2)
hold on
plot(time,x4b,'r--','linewidth',2)
xlabel('time/s');
ylabel('x''');
grid on
legend('控制率函数1','控制率函数2');
axis([20,80,-1.2e-2,1.2e-2]);
figure;
plot(time,x5a,'linewidth',2)
hold on
plot(time,x5b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_1''');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x5a,'linewidth',2)
hold on
plot(time,x5b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_1''');
grid on
legend('控制率函数1','控制率函数2');
axis([20,100,-5e-2,5e-2]);
figure;
plot(time,x6a,'linewidth',2)
hold on
plot(time,x6b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_2''');
grid on
legend('控制率函数1','控制率函数2');
figure;
plot(time,x6a,'linewidth',2)
hold on
plot(time,x6b,'r--','linewidth',2)
xlabel('time/s');
ylabel('\theta_2''');
grid on
legend('控制率函数1','控制率函数2');
axis([20,80,-15e-3,15e-3]);
08_082_m





































