1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Zl5xs
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
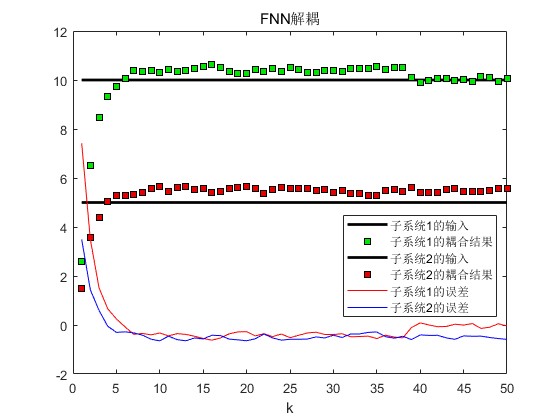
3.算法概述
系统的复杂性与所要求的精确性之间存在尖锐矛盾,为此,通过模拟人类学习和自适应能力,人们提出了智能控制的思想。控制理论专家Austrom(1991)在IFAC 大会上指出:模糊逻辑控制、神经网络与专家控制是三种典型的智能控制方法。通常专家系统建立在专家经验上,并非建立在工业过程所产生的操作数据上,且一般复杂系统所具有的不精确性、不确定性就算领域专家也很难把握,这使建立专家系统非常困难。而模糊逻辑和神经网络作为两种典型的智能控制方法,各有优缺,模糊逻辑与神经网络的融合———模糊神经网络(Fuzzy Neural Network)由于吸取了模糊逻辑和神经网络的优点, 部分避免了两者的缺点, 已经成为当今智能控制研究的热点之一。
4.部分源码
..........................................................................
%子系统1(SUB1)的J循环开始
for J=1:50
ep1=10-yp1;
pid=kp*(ep1-ep0)+ki*ep1;
up2=up1+pid;
yp2=0.5*yp1+2.5*up2+2.5*up1;
yp(:,J)=yp2;
up0=up1;
up1=up2;
ep0=ep1;
yp0=yp1;
yp1=yp2;
end
..........................................................................
%输出
sum=0;
for i=1:3
for j=1:3
sum=sum+h(i,j)*v1(i,j);
end
end
ot=sum;cu=su*ot;u2=u1+cu;disp(u2);
if(u2<0)
u2=0;
elseif(u2>=1)
u2=1;
end
y2=0.5*y1+2.5*u2+2.5*u1+n1(:,k)+0.01*y12;
%+n1(:,k)+0.01*y12表示随机噪声和子系统间的相互耦合
disp(['the output y number is' int2str(T)]);
disp(y2);
Y(:,k)=y2;E=0.5*(sp-y2).^2;e2=sp-y2;
Es(:,k)=e2;
x1=e2;x2=e2-e1;e0=e1;e1=e2;
delot=(sp-y2)*2.5*su;
for i=1:3
for j=1:3
dv=v1(i,j)-v0(i,j);
v2=v1(i,j)+p13*delot+q13*dv;
v3(i,j)=v2;
end
end
.......................................................
end
if(abs(e1)<=eps & abs(e)<=eps)
break;
else
k=k+1;
end
y02=y12;y12=y22;u02=u12;u12=u22;
end
L=k-1; n2=n;
%L=k;
m=1:L;
R=ones(size(m));
sp=R*10;sp2=R*5;
figure
plot(m,sp,'k','LineWidth',2);
hold on
plot(m,Y,'bs',...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.0,0.9,0.0]);
hold on
plot(m,sp2,'k','LineWidth',2);
hold on
plot(m,Y2,'rs',...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
plot(m,Es,'r');
hold on
plot(m,E22,'b');
legend('子系统1的输入','子系统1的耦合结果','子系统2的输入','子系统2的耦合结果','子系统1的误差','子系统2的误差' );
%图标炷
title('FNN解耦'),
xlabel('k'),
figure
plot(m,n1,'b--',m,n2,'r');
legend('子系统1的噪声','子系统2的噪声' ); %图标炷
xlabel('k'),
A316





































