1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qbmZtx
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
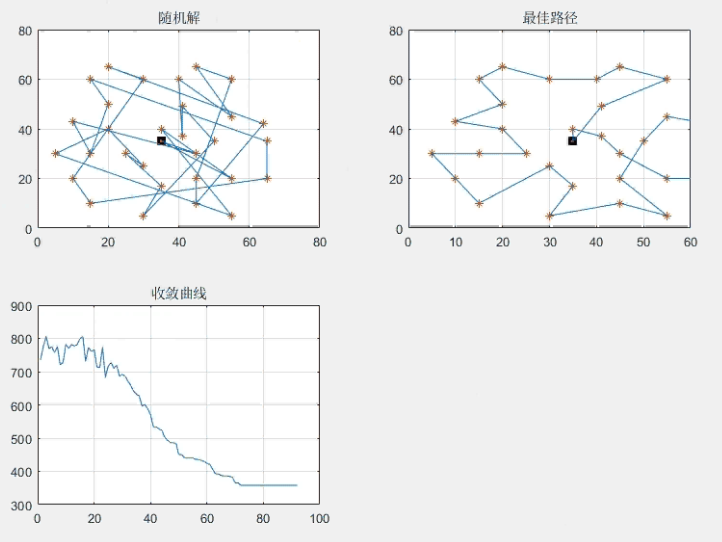
3.算法概述
粒子群优化算法(PSO)是一种进化计算技术(evolutionary computation),1995 年由Eberhart 博士和kennedy 博士提出,源于对鸟群捕食的行为研究 。该算法最初是受到飞鸟集群活动的规律性启发,进而利用群体智能建立的一个简化模型。粒子群算法在对动物集群活动行为观察基础上,利用群体中的个体对信息的共享使整个群体的运动在问题求解空间中产生从无序到有序的演化过程,从而获得最优解。
粒子群算法,也称粒子群优化算法或鸟群觅食算法(Particle Swarm Optimization),缩写为 PSO, 是近年来由J. Kennedy和R. C. Eberhart等开发的一种新的进化算法(Evolutionary Algorithm - EA)。PSO 算法属于进化算法的一种,和模拟退火算法相似,它也是从随机解出发,通过迭代寻找最优解,它也是通过适应度来评价解的品质,但它比遗传算法规则更为简单,它没有遗传算法的“交叉”(Crossover) 和“变异”(Mutation) 操作,它通过追随当前搜索到的最优值来寻找全局最优。这种算法以其实现容易、精度高、收敛快等优点引起了学术界的重视,并且在解决实际问题中展示了其优越性。粒子群算法是一种并行算法。
PSO初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次的迭代中,粒子通过跟踪两个“极值”(pbest,gbest)来更新自己。在找到这两个最优值后,粒子通过下面的公式来更新自己的速度和位置。
4.部分源码
.........................................
MI=100; %最大迭代次数
IsStop=0;
INUM=0; %当适应值不变的时候,INUM+1计数,到20时就结束迭代
c1=0.1;
c2=5;
w=0.96;
load 'node.txt';
xy=node(2:NUM+1,2:3);
x0=ones(N,NUM);
for i=1:N %随机给每个粒子分配路径
x0(i,:)=randperm(NUM);
end
v0=zeros(N,NUM);
for i=1:N %在VRP中粒子的速度代表交换序
v0(i,:)=round(rand(1,NUM)*NUM);
end
distance_center=zeros(1,NUM);%每个粒子离配送中心的距离
for i=1:NUM
distance_center(i)=sqrt((node(i+1,2)-node(1,2))^2+(node(i+1,3)-node(1,3))^2);
end
distance_two=zeros(NUM,NUM); %每两个用户之间的距离
for i=1:NUM-1
for j=i+1:NUM
dis=sqrt((xy(i,1)-xy(j,1))^2+(xy(i,2)-xy(j,2))^2);
distance_two(i,j)=dis;
distance_two(j,i)=dis;
end
end
for i=1:N %每个粒子路径的总距离
EachPathDis(i)=PathDistance(x0(i,:),distance_two,distance_center);
end
IBest=x0; %粒子个体的历史最优路径
IBestFitness=EachPathDis;%粒子个体的历史最优适应值
[GBestFitness,index]=min(EachPathDis); %粒子全局最优路径
g1=GBestFitness; %粒子全局最优适应值
figure;
subplot(2,2,1);
PathPlot(node,NUM,index,IBest);
title('随机解');
while(IsStop==0)&&(Iteration<MI)
Iteration=Iteration+1;
%g2(Iteration)=GBestFitness;
for i=1:N
GBest(i,:)=x0(index,:); %全局最优路径
end
pi_x=GenerateChangeNums(x0,IBest); %(Pi-Xi)就是使xi向个体最优解靠近,而非远离,这也是一个交换用户序号的过程,得到交换的序
pi_x=HoldByOdds(pi_x,c1); %这是c1*(Pi-Xi)的过程,以c1保留交换序
pg_x=GenerateChangeNums(x0,GBest); %(Pg-Xi)就是使Xi向全局最优解靠近,得到路径中要交换的用户序号
pg_x=HoldByOdds(pg_x,c2); %这是c2*(Pg-Xi)的过程,以c2保留交换序
v0=HoldByOdds(v0,w); %这是w*Vi的过程,以概率w得到交换序
x0=PathExchange(x0,v0); %通过交换序来改变每个粒子的路径,也就是优化的过程
x0=PathExchange(x0,pi_x);
x0=PathExchange(x0,pg_x);
for i=1:N %计算每条路径的距离
EachPathDis(i)=PathDistance(x0(i,:),distance_two,distance_center);
end
IsChange=EachPathDis<IBestFitness; %更新后的距离优于更新前的,记录序号
IBest(find(IsChange),:)=x0(find(IsChange),:); %更新个体最佳路径
IBestFitness=IBestFitness.*(~IsChange)+EachPathDis.*IsChange; %更新个体最佳路径距离
[GBestFitness,index]=min(EachPathDis); %更新全局最佳路径,记录相应的序号
if GBestFitness==OldpgFitness %比较更新前和更新后的适应度值;
INUM=INUM+1;
else
OldpgFitness=GBestFitness; %不相等时更新适应度值,并记录清零
INUM=0;
end
....................................................
A146





































