1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Wmp1p
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览

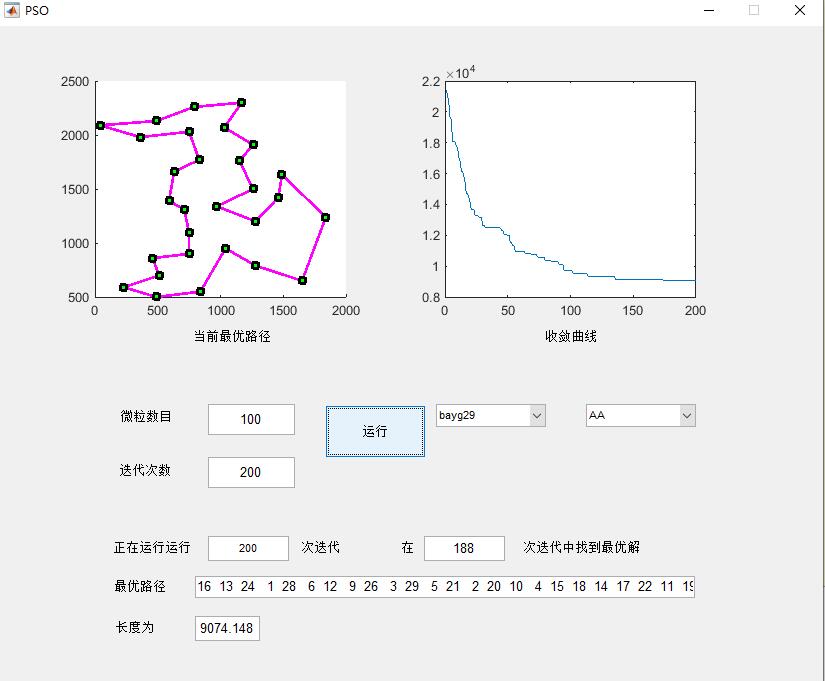
3.算法概述
PSO从这种模型中得到启示并用于解决优化问题。PSO中,每个优化问题的解都是搜索空间中的一只鸟。我们称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值(fitnessvalue),每个粒子还有一个速度决定他们飞翔的方向和距离。然后粒子们就追随当前的最优粒子在解空间中搜索。
粒子群优化算法(PSO),粒子群中的每一个粒子都代表一个问题的可能解, 通过粒子个体的简单行为,群体内的信息交互实现问题求解的智能性。
在求解TSP这种整数规划问题的时候, PSO显然与ACO不同, PSO需要对算法本身进行一定的修改, 毕竟PSO刚开始是应用在求解连续优化问题上的.
4.部分源码
.........................................................................
% nummin=xulie(Pb) %最小适应度种群序号
a1=Pb(1);
a2=1;
for i=1:m
if a1>=Pb(i)
a1=Pb(i);
a2=i;
end
end
nummin=a2;
Gb(N)=Pb(nummin); %当前群体最优长度
for i=1:m
%% 与个体最优进行交叉
c1=round(rand*(n-2))+1; %在[1,n-1]范围内随机产生一个交叉位
c2=round(rand*(n-2))+1;
while c1==c2
c1=round(rand*(n-2))+1; %在[1,n-1]范围内随机产生一个交叉位
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=Tour_pbest(i,chb1:chb2); %交叉区域矩阵
ncros=size(cros,2); %交叉区域元素个数
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
xnew=xnew1;
%插入交叉区域
for j=1:ncros
xnew1(i,n-ncros+j)=cros(j);
end
%判断产生新路径长度是否变短
dist=0;
for j=1:n-1
dist=dist+D(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+D(xnew1(i,1),xnew1(i,n));
if F(i)>dist
x(i,:)=xnew1(i,:);
end
%% 与全体最优进行交叉
c1=round(rand*(n-2))+1; %在[1,n-1]范围内随机产生一个交叉位
c2=round(rand*(n-2))+1;
while c1==c2
c1=round(rand*(n-2))+1; %在[1,n-1]范围内随机产生一个交叉位
c2=round(rand*(n-2))+1;
end
chb1=min(c1,c2);
chb2=max(c1,c2);
cros=Tour_gbest(chb1:chb2); %交叉区域矩阵
ncros=size(cros,2); %交叉区域元素个数
%删除与交叉区域相同元素
for j=1:ncros
for k=1:n
if xnew1(i,k)==cros(j)
xnew1(i,k)=0;
for t=1:n-k
temp=xnew1(i,k+t-1);
xnew1(i,k+t-1)=xnew1(i,k+t);
xnew1(i,k+t)=temp;
end
end
end
end
xnew=xnew1;
%插入交叉区域
for j=1:ncros
xnew1(i,n-ncros+j)=cros(j);
end
%判断产生新路径长度是否变短
dist=0;
for j=1:n-1
dist=dist+D(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+D(xnew1(i,1),xnew1(i,n));
if F(i)>dist
x(i,:)=xnew1(i,:);
end
%% 进行变异操作
c1=round(rand*(n-1))+1; %在[1,n]范围内随机产生一个变异位
c2=round(rand*(n-1))+1;
temp=xnew1(i,c1);
xnew1(i,c1)=xnew1(i,c2);
xnew1(i,c2)=temp;
%判断产生新路径长度是否变短
dist=0;
for j=1:n-1
dist=dist+D(xnew1(i,j),xnew1(i,j+1));
end
dist=dist+D(xnew1(i,1),xnew1(i,n));
%dist=dist(xnew1(i,:),D);
if F(i)>dist
x(i,:)=xnew1(i,:);
end
end
% F=(x,C,D) %计算种群适应度
%xuhao=xulie(F) %最小适应度种群序号
a1=F(1);
a2=1;
for i=1:m
if a1>=F(i)
a1=F(i);
a2=i;
end
end
xuhao=a2;
.........................................................................
end
A252





































