1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJeTk5pu
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
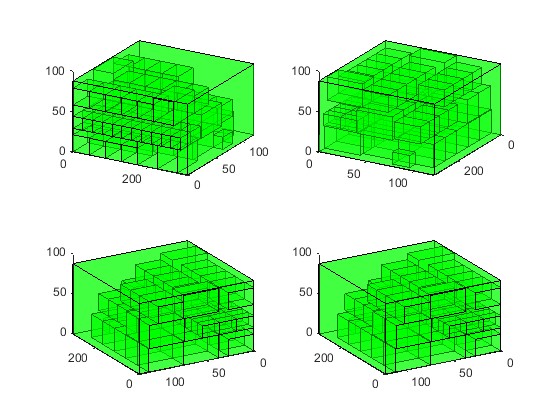

3.算法概述
模拟退火算法(Simulated Annealing,SA)最早的思想是由N. Metropolis [1] 等人于1953年提出。1983 年,S. Kirkpatrick 等成功地将退火思想引入到组合优化领域。它是基于Monte-Carlo迭代求解策略的一种随机寻优算法,其出发点是基于物理中固体物质的退火过程与一般组合优化问题之间的相似性。模拟退火算法从某一较高初温出发,伴随温度参数的不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解,即在局部最优解能概率性地跳出并最终趋于全局最优。模拟退火算法是一种通用的优化算法,理论上算法具有概率的全局优化性能,目前已在工程中得到了广泛应用,诸如VLSI、生产调度、控制工程、机器学习、神经网络、信号处理等领域。
4.部分源码
..........................................................................
%重构箱子box: 重 长 宽 高 体积
for i=1:size(box,1)
box(i,5)=prod(box(i,2:4),2);
end
num_cargo = size(cargo,1); % 货物数
num_box = size(box,1); % 货箱数
solution= fix((num_box)*rand(1,num_cargo))+1; %随机生成初始解
Scheme=transform(solution); %解转化成“货箱:货物”对应的形式
[feas_solution,Scheme]= placement(Scheme); %装箱处理
[PG,PV,gbest ]= evaluate(feas_solution) ; %计算适应度
%退火
begin = cputime;
[final_solution,gbest] = GENE(pop,maxite,num_cargo,pm) ;
%模拟退火进一步优化
T = T0;
Ra = [];
Rb = [];
Rc = [];
while T > T_End
T
for i=1:metropolis
newsolution=final_solution;
R1=fix(rand*num_cargo)+1;
R2=fix(rand*num_cargo)+1;
inter=newsolution(R1);
newsolution(R1)=newsolution(R2);
newsolution(R2)=inter;
NewScheme=transform(newsolution); % 分配货箱
[feas_solution,NewScheme]= placement(NewScheme); % 装箱处理
[NPG,NPV,pbest ]= evaluate(feas_solution); % 评估新方案
if pbest>gbest
gbest = pbest;
final_solution = newsolution;
PG = NPG;
PV = NPV;
Scheme = NewScheme;
else
if rand < exp( (pbest-gbest)*100*T0/T)
gbest=pbest;
final_solution=newsolution;
PG = NPG;
PV = NPV;
Scheme = NewScheme;
end
end
end
T = T * cooling;
Ra = [Ra,gbest];
Rb = [Rb,PG];
Rc = [Rc,PV];
end
t1=smooth(Ra,32);
t2=smooth(Rb,32);
t3=smooth(Rc,32);
figure;
plot(1:10:length(Ra),t1(1:10:end),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
legend('重量利用率');
figure;
plot(1:10:length(Rb),t2(1:10:end),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
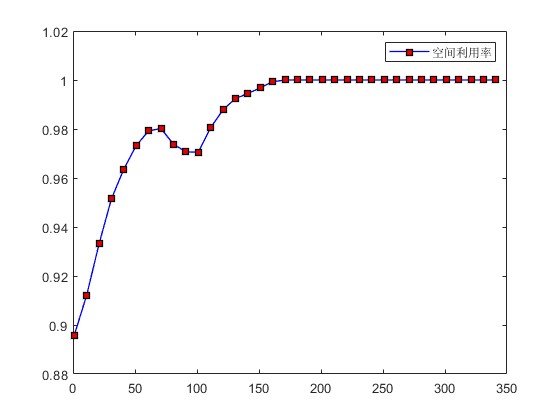
legend('空间利用率');
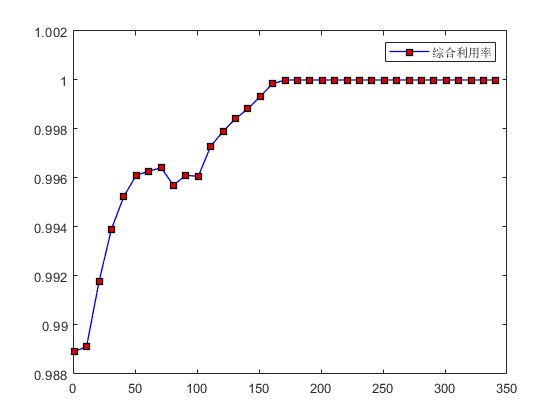
figure;
plot(1:10:length(Rc),t3(1:10:end),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
legend('综合利用率');
A567
....................................................................





































