1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52cm51t
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
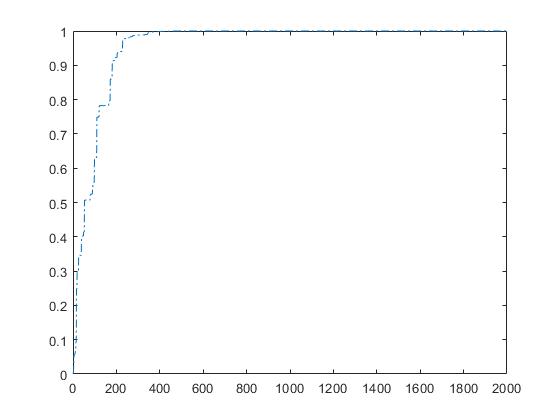
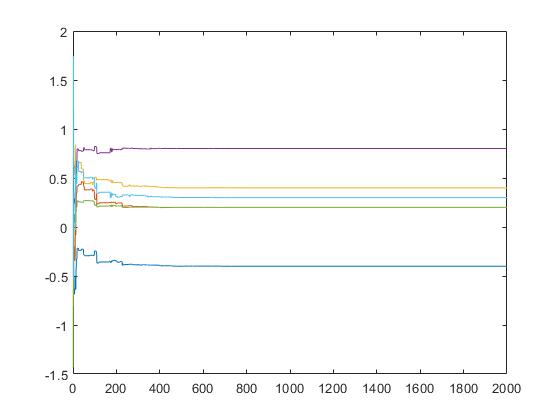
3.算法概述
粒子群优化算法(PSO),粒子群中的每一个粒子都代表一个问题的可能解, 通过粒子个体的简单行为,群体内的信息交互实现问题求解的智能性。ARIMAX模型是指带回归项的ARIMA模型,又称扩展的ARIMA模型。回归项的引入有利于提高模型的预测效果。引入的回归项一般是与预测对象(即被解释变量)相关程度较高的变量。比如分析居民的消费支出序列时,消费会受到收入的影响,如果将收入也纳入到研究范围,就能够得到更精确的消费预测。
4.部分源码
% 用标准PSO辨识NARMAX模型
var=0.001; % 噪声方差
% iter_max=Nc_max*4;
err=0.01;
iter_max=2000; % 最大迭代次数
L=15; % 窗口宽度
N=30; % 种群规模
C1=2; % 加速度常数
C2=C1;
Xmin=-3; % 解取值范围[Xmin,Xmax]
Xmax=3;
p=6; % 粒子维数
w=linspace(0.9,0.5,iter_max); % 惯性权重
X=Xmin+(Xmax-Xmin)*rand(p,N); % 粒子位置
Xpbest=X; % 个体最佳位置
Xgbest=Xmin+(Xmax-Xmin)*rand(p,1); % 种群最佳位置
fpbest=0*rand(1,N); % 个体最佳适应度值
fgbest=0; % 种群最佳适应度值
fgbest_fig=zeros(1,iter_max);
Xgbest_fig=zeros(p,iter_max);
Vmax=(Xmax-Xmin)*0.2;
V=Vmax*(2*rand(p,N)-1);
u=idinput(L,'rgs',[0 1],[-1 1]); % 随机白噪声序列,取L个,均值为0,方差为1
e=idinput(L,'rgs',[0 1],[-var var]); % 高斯白噪声,均值为0,方差为var
theta0=[-0.4 0.2 0.4 0.8 0.2 0.3]; % 待辨识参数真值
%-----------------------------------------------output of theoretical value
y0(1:4)=0;
y(1:4)=0;
for k=5:L
y0(k)=theta0*[y0(k-1) y0(k-2)*y0(k-3) y0(k-4) u(k-1)^3 y0(k-2)^2 u(k-3)]'+e(k);
end
%----------------------------------------------------------------------main
iter=0;
while iter<iter_max
iter=iter+1;
for i=1:N
for k=5:L
y(k)=X(:,i)'*[y(k-1) y(k-2)*y(k-3) y(k-4) u(k-1)^3 y(k-2)^2 u(k-3)]';
end
J=1/(1+(y-y0)*(y-y0)');
if J>fpbest(i)
fpbest(i)=J;
Xpbest(:,i)=X(:,i);
end
end
[fitnessmax,index]=max(fpbest);
if fitnessmax>fgbest
fgbest=fitnessmax;
Xgbest=X(:,index);
end
for i=1:N
r1=rand;
r2=rand;
fai1=C1*r1;
fai2=C2*r2;
% 速度更新
V(:,i)=w(iter)*V(:,i)+fai1*(Xpbest(:,i)-X(:,i))+fai2*(Xgbest(:,1)-X(:,i));
% 若速度超过限定值,则让其等于边界值
index=find(abs(V(:,i))>Vmax);
if(any(index))
V(index,i)=V(index,i)./abs(V(index,i)).*Vmax;
end
% 位置更新
X(:,i)=X(:,i)+V(:,i);
end
fgbest_fig(iter)=fgbest;
Xgbest_fig(:,iter)=Xgbest;
end
A183





































