1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5uUk5hs
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
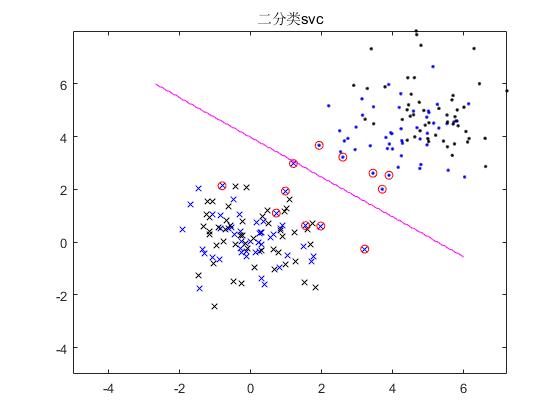
3.算法概述
SVM是一种二分类模型,该模型是定义为特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM 还包括核技巧,这使它成为实质上的非线性分类器。其学习策略就是间隔最大化,可形式化为一个求解凸二次规划的最小化问题。
4.部分源码
......................................................
%%=========================================================================
%定义核函数及相关参数
C =0.1719;
ker=struct('type','linear');
%%=========================================================================
%构造训练样本和训练目标
n = 50;
% randn('state',2);%选择正态分布数据,线性可分样本点
x1 = randn(n,2);
y1 = ones(n,1);
x2 = 4+randn(n,2);
y2 = -ones(n,1);
X = [x1;x2]; % 训练样本,2n×2的矩阵,2n为样本个数,2为样本维数
Y=[y1;y2];
% figure(2)
% plot(x1(:,1),x1(:,2),'x')
figure();
plot(x1(:,1),x1(:,2),'bx',x2(:,1),x2(:,2),'b.');
title('二分类svc');
hold on;
% 构造测试样本
x3 = randn(n,2);
x4 = 5+randn(n,2);
Xd = [x3;x4];
plot(x3(:,1),x3(:,2),'kx',x4(:,1),x4(:,2),'k.');
hold on
...........................................
A156





































