1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qZmp1t
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
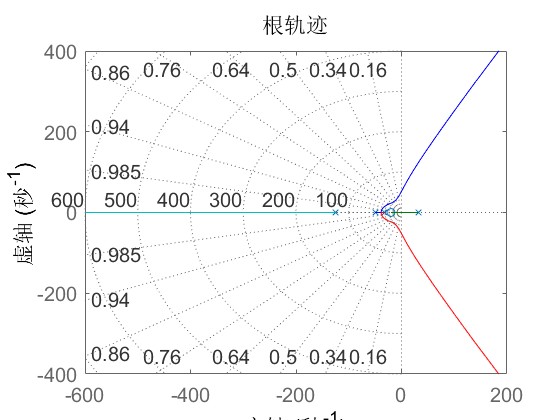
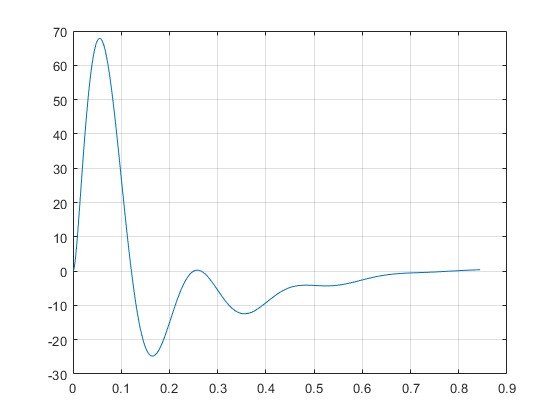
3.算法概述
在磁悬浮的许多实际应用中,都要求磁悬浮系统的悬浮气隙有较大的工作范围。但由于磁悬浮力-电流-气隙之间的非线性特性,系统模型开环不稳定。至少需要输出反馈进行闭环控制,才能够实现稳定悬浮。为了设计一个性能良好的悬浮控制器,基于磁悬浮系统的稳定性控制问题受到了广泛而又深入的研究。传统工业控制中多采用成熟的PID控制调节器,其中比例环节可以加快系统反应速度,积分环节可以消除静差,调节系统刚度;微分环节可以调节系统阻尼特性,改善系统的动态品质。
4.部分源码
clc;
clear;
close all;
y=MagLev;
yy=pole(y);
PD=tf(-1*[1 20],[1 50]);
rlocus(PD*MagLev);
PI=tf([1 1],[1 0]);
[y,t]=impulse(feedback(150*PI*PD*MagLev,1));
sgrid;
figure(2);
plot(t,y)
grid;
v0=0.991;h0=0.02;
[num,den]=tfdata(150*PD*PI,'v');
simulink;
function[sys,x0]=MagModel(t,x,u,flag)
m=0.1;
g=9.82;
R=5;
L=0.04;
k=0.01;
h0=0.02;
i0=h0*sqrt(m*g/k);
switch flag,
case 1,
xdot =zeros(3,1);
xdot(1)=x(2);
xdot(2)=m*g-k*x(3)^2/x(1)^2;
xdot(3)=-R/L*x(3)+1/L*u(1);
sys=xdot;
case 3,
sys=x(1);
case 0,
sys==[3 0 1 1 0 0];
x0=[h0+0.1*h0;0;i0];
otherwise
sys=[];
end
A135





































