1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qTlJxu
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
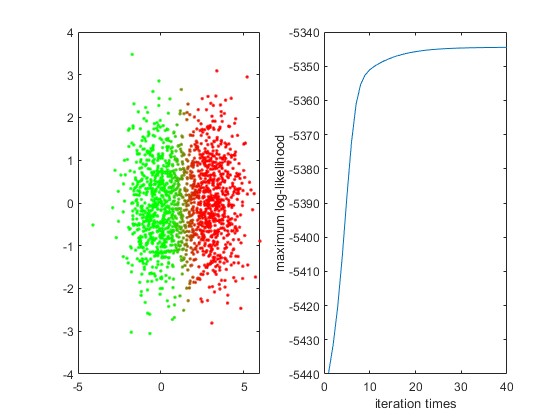
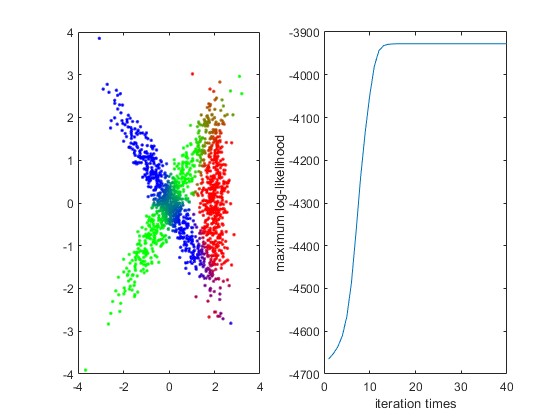
3.算法概述
EM(Expectation-Maximum)算法也称期望最大化算法,曾入选“数据挖掘十大算法”中,可见EM算法在机器学习、数据挖掘中的影响力。EM算法是最常见的隐变量估计方法,在机器学习中有极为广泛的用途,例如常被用来学习高斯混合模型(Gaussian mixture model,简称GMM)的参数;隐式马尔科夫算法(HMM)、LDA主题模型的变分推断等等。本文就对EM算法的原理做一个详细的总结。
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation-Maximization Algorithm),最初是为了解决数据缺失情况下(包含隐变量)的参数估计问题。
其基本思想是:首先根据己经给出的观测数据,估计出模型参数的值(初始化);然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束。
EM算法是一种迭代优化策略,由于它的计算方法中每一次迭代都分两步,其中一个为期望步(E步),另一个为极大步(M步),所以算法被称为EM算法(Expectation-Maximization Algorithm)。EM算法受到缺失思想影响,最初是为了解决数据缺失情况下的参数估计问题,其算法基础和收敛有效性等问题在Dempster、Laird和Rubin三人于1977年所做的文章《Maximum likelihood from incomplete data via the EM algorithm》中给出了详细的阐述。其基本思想是:首先根据己经给出的观测数据,估计出模型参数的值;然后再依据上一步估计出的参数值估计缺失数据的值,再根据估计出的缺失数据加上之前己经观测到的数据重新再对参数值进行估计,然后反复迭代,直至最后收敛,迭代结束。
4.部分源码
function [gamma,llm]=em1r(r,k)
load ('data.mat')
x=dataset1;
L=size(x);
l=L(1);
zc=zeros(r,40);llm=-inf;
for zzz=1:r
sigma=zeros(2,2,k);
mu=zeros(k,2);
sigma(:,:,1)=cov(x);
n=zeros(1,3);
pik=ones(k,1)/k;
while (~(n(1)~=n(2)&&n(2)~=n(3)&&n(3)~=n(1)))
n=ceil(rand(1,3)*1500);
end
for ii=1:k
mu(ii,:)=x(n(ii),:);
sigma(:,:,ii)=sigma(:,:,1);
end
for zz=1:40
p=zeros(l,k);
for ii=1:k
p(:,ii)=mvnpdf(x,mu(ii,:),sigma(:,:,ii));
end
gamma=zeros(l,k);
for ii=1:l
su=0;
for jj=1:k
su=pik(jj)*p(ii,jj)+su;
end
for jj=1:k
gamma(ii,jj)=pik(jj)*p(ii,jj)/su;
end
end
nk=zeros(k,1);
for ii=1:k
nk(ii)=sum(gamma(:,ii));
end
pik=nk/l;
for ii=1:k
mu(ii,1)=sum(gamma(:,ii).*x(:,1))/nk(ii);
mu(ii,2)=sum(gamma(:,ii).*x(:,2))/nk(ii);
end
ssig=zeros(2,2,l);
for ii=1:k
for jj=1:l
ssig(:,:,jj)=gamma(jj,ii).*(x(jj,:)-mu(ii,:))'*(x(jj,:)-mu(ii,:));
end
sigma(1,1,ii)=sum(ssig(1,1,:))/nk(ii);
sigma(1,2,ii)=sum(ssig(1,2,:))/nk(ii);
sigma(2,1,ii)=sum(ssig(2,1,:))/nk(ii);
sigma(2,2,ii)=sum(ssig(2,2,:))/nk(ii);
end
ll=0;
for ii=1:l
bb=0;
for jj=1:k
bb=bb+pik(jj)*mvnpdf(x(ii,:),mu(jj,:),sigma(:,:,jj));
end
ll=ll+log(bb)/log(exp(1));
end
zc(zzz,zz)=ll;
end
if llm<ll
llm=ll;
mii=zzz;
gam=gamma;
end
end
colo=zeros(l,3);
colo(:,1:2)=gam;
figure
subplot(1,2,1);
for ii=1:l
plot(x(ii,1),x(ii,2),'.','color',colo(ii,:));
hold on
end
hold off;
subplot(1,2,2)
plot(1:40,zc(mii,:));
xlabel('iteration times')
ylabel('maximum log-likelihood')
end
A118





































