1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52ZmJps
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
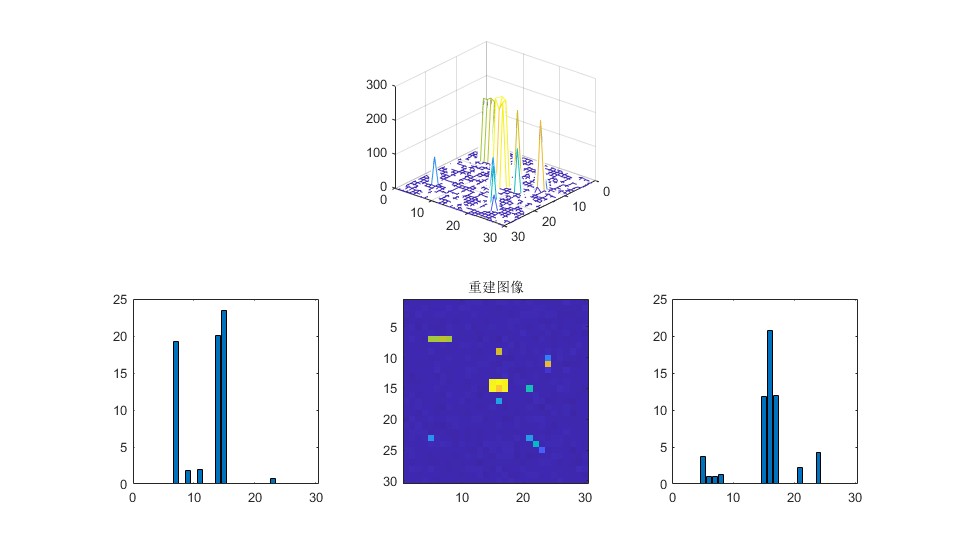
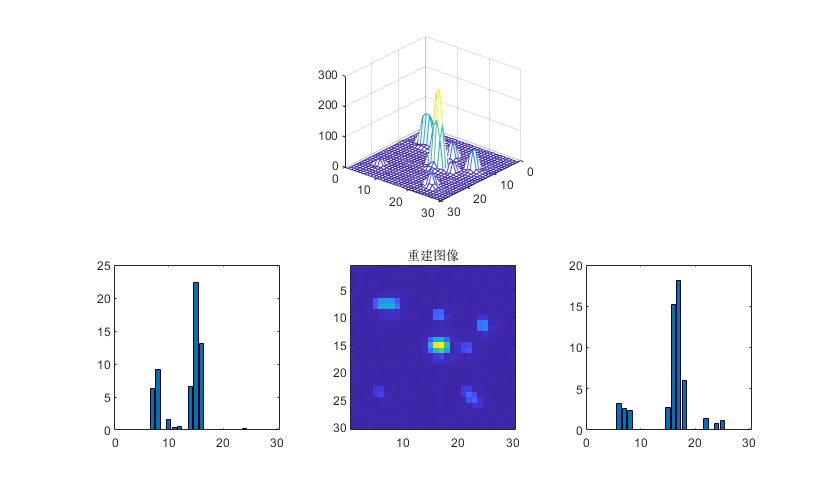
3.算法概述
超分辨率(Super-Resolution)通过硬件或软件的方法提高原有图像的分辨率,通过一系列低分辨率的图像来得到一幅高分辨率的图像过程就是超分辨率重建。超分辨率成像(SR-imaging)是提高成像系统分辨率的一类技术。光学SR技术可以超越系统的衍射极限,而几何SR则可以提高数字成像传感器的分辨率。超分辨率成像技术广泛应用于图像处理和超分辨显微术中。
超分辨率贝叶斯法即PanSharpening方法,该方法利用全色波段增强多光谱遥感影像,合并传感器特性模拟了全色波段和多波段影像的观测过程,利用先验知识估计高分辨率多光谱影像的期望值。基于贝叶斯理论的重构算法的研究发展迅速,它利用少量的先验知识,通过贝叶斯理论和参数优化方法得到后验分布并最终重构出原始信号.在传统贝叶斯重构算法的基础上,将信号自身固有的结构特征与贝叶斯重构算法相结合,分别对单传感器获取的信号,多传感器获取的信号进行重构,然后通过最大期望算法对参数进行优化.概率建模是一种发现数据中潜在规律的重要方法,概率模型通过一组假设来分析数据,但倘若数据偏离了假设就会给我们的推断和预测带来威胁。
4.部分源码
%这里为了对比两个算法的性能差异,因此最大程度的简化了信源的建模。直接模拟产生阵列接收到的信号进行仿真测试
load test.mat
SNR = 0;
sigma = 10^(-SNR/10);
I1 = I1 + sigma*randn(size(I1));
object = func_Bayesian_super_resolution(I1);
II = object;
[X,Y]=size(II);
[Xs,Ys]=meshgrid(1:X,1:Y);
%显示结果
figure
subplot(232);
mesh(Ys,Xs,double(II));
view([130,30]);
axis([0,30,0,30,0,300]);
subplot(234);
t1 = mean(II,2)-5;
t1(find(t1<0))=0;
bar(t1);
axis square;
subplot(235);
imagesc(II);
title('重建图像');
axis square;
subplot(236);
t2 = mean(II,1)-5;
t2(find(t2<0))=0;
bar(t2);
axis square;
05_019_m





































