1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52ZmJly
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
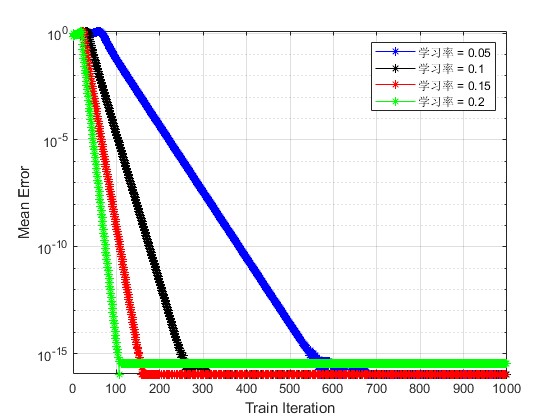
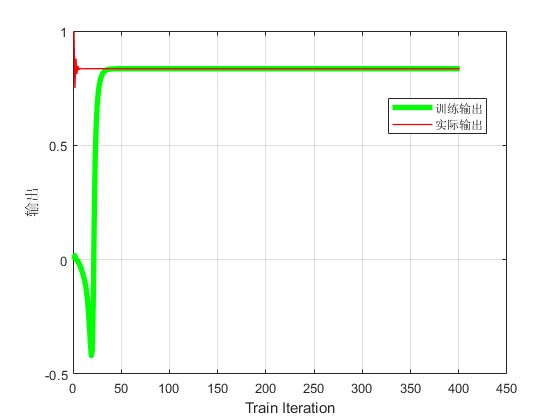
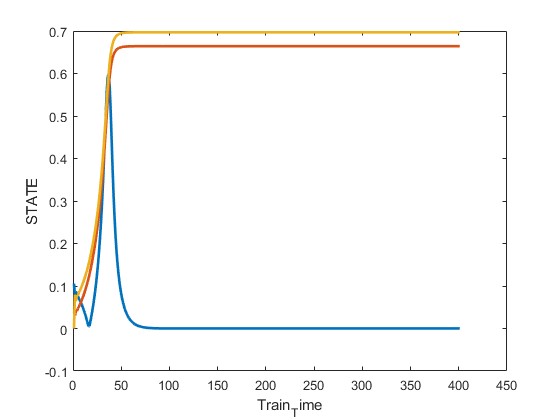
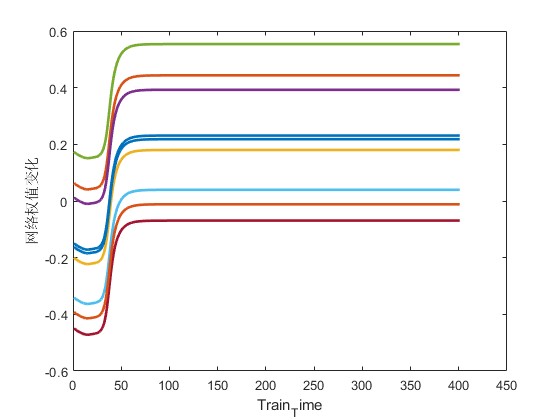
3.算法概述
GNNs是基于信息扩散机理。一个图被处理为一系列单元,每个相当于图的节点,他们根据图的连通性联结着。这些单元刷新它们的状态并交换信息直到它们达到稳定平衡。之后基于单元的状态,GNN的输出可以在节点层间计算出。扩散机理的限制使得一个独特的稳定平衡总是存在。这种认识机制已被用在蜂窝神经网络及Hopfield神经网络。在这些神经网络模型中,连通性根据预定义的图描述,网络的连接自然属性上是循环周期性的,神经元的状态通过达到一个平衡点来计算。GNNs有别于蜂窝神经网络及Hopfield神经网络在于它们可以用在处理更广泛类型的图,如无向图,并且它们采用更综合的扩散机制。
4.部分源码
Nodes = [40:5:200];
Index = 0;
for nn = 1:length(Nodes)
Nodes(nn)
tic;
Index = Index + 1;
%初始参数
%学习率
Learn_rate = 0.2;
%惯性
lemda = 0.01;
%网络结构参数
Num_I = 40;
Num_Hide = 120;
Num_O = 1;
%训练次数
Train_Time = 40;
%初始化神经元输入信号
dw = cell(1,Num_I);
delta = [zeros(1,Num_Hide)];
x = [zeros(1,Num_I)];
Yout = 0;
du = 0;
Yout_Delay = zeros(1,Num_I);
l = zeros(1,Num_I);
%隐藏层神经元的输出
Oh = zeros(Num_Hide,1);
I = Oh;
Oh_delay = Oh;
%初始化突触权值参数
Net = func_initialize(Num_I,Num_Hide,Num_O);
%forward
x = func_forward(Net,l);
k = 0;
while(k <= Train_Time | k <= Nodes(nn))
k = k + 1;
%模拟训练数据和训练目标
P(k) = 1;
Yout(k) = (0.5*Yout_Delay(1)+P(k))/(1 + Yout_Delay(1)^2);
[Yout_Est(k),I,Oh] = func_backward(x,Net,Oh_delay,Num_Hide);
Err(k) = Yout(k) - Yout_Est(k);
%Jacobian
Jacobian_out(k) = func_Jacobian(Net,delta,Num_Hide);
%更新网络系数w
[Net,dw,delta] = func_w_update(x,I,Net,dw,Err(k),Learn_rate,lemda,Oh,Oh_delay,Num_I,Num_Hide);
%FORWARD
l = [Err(k),Yout(k),Yout_Delay(1:end-2)];
x = func_forward(Net,l);
%Delay;
Yout_Delay(1) = Yout(k);
for idx = 2:Num_I
Yout_Delay(idx)=Yout_Delay(idx-1);
end
Net.wd2{1} = Net.wd1{1};
Net.wd1{1} = Net.w{1};
Net.wd2{3} = Net.wd1{3};
Net.wd1{3} = Net.w{3};
Net.wd2{2} = Net.wd1{2};
Net.wd1{2} = Net.w{2};
end
toc;
time(Index) = toc;
end
05_017_m





































