1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZpWVlpxq
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
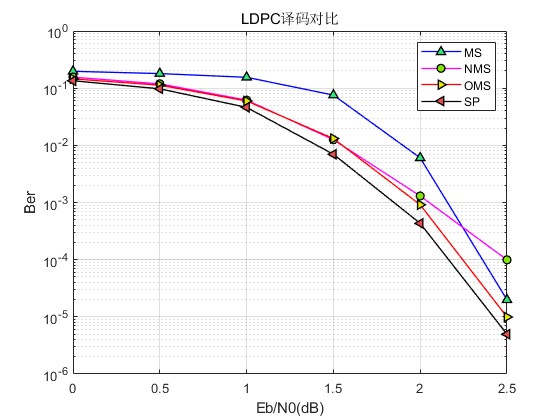
3.算法概述
低密度奇偶校验码(LDPC)译码是现代通信系统中一种高效的错误校正技术,广泛应用于无线通信、卫星通信和数据存储等领域。LDPC码因其良好的纠错性能和接近香农极限的潜力而受到重视。本文将详细对比四种主流的迭代译码算法:Sum-Product (SP)、Min-Sum (MS)、Normalized Min-Sum (NMS) 和 Offset Min-Sum (OMS)。
4.部分源码
..........................................................
for jj = 1:1:length(SNR)
%仿真帧
Frames = 50;
error1 = 0;
cout = 0;
sigma = sqrt(1/10^(SNR(jj)/10));
for i = 1:1:Frames
[i,SNR(jj) ]
%编码
msg = randi([0, 1], 1, 1008);
msg_encode = func_Encoder(Hs, msg);
%调制
bpsk_encode = 1 - 2.*msg_encode;
%AWGN
bpsk_N = awgn(bpsk_encode,SNR(jj),'measured');
%接收
llr = 2*bpsk_N/(sigma^2);
ydecode = func_MS( H, llr, Iters );
errs = sum(msg ~= ydecode);
error1 = error1 + errs;
cout = cout + 1;
end
Ber(1, jj) = error1/(K * cout);
end
figure
semilogy(SNR, Ber,'-b^',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.2,0.9,0.5]);
xlabel('Eb/N0(dB)');
ylabel('Ber');
title('最小和MS')
grid on;
save MS.mat SNR Ber
0X_051m
---





































