1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5uTmJ5w
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
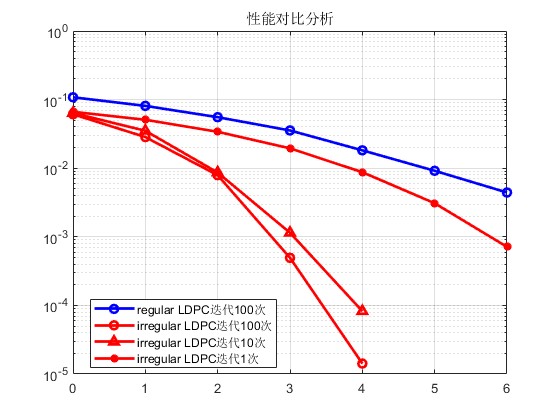
3.算法概述
LDPC码是麻省理工学院Robert Gallager于1963年在博士论文中提出的一种具有稀疏校验矩阵的分组纠错码。几乎适用于所有的信道,因此成为编码界近年来的研究热点。它的性能逼近香农极限,且描述和实现简单,易于进行理论分析和研究,译码简单且可实行并行操作,适合硬件实现。
LDPC 码可以通过校验矩阵 H 来唯一确定,校验矩阵 H 是大小为m*n 的稀疏矩阵,其中m 为校验位长度,n 为 LDPC 码码长,信息位长度为 k =n-m 。LDPC 码可以分为规则 LDPC 码和非规则 LDPC 码两种[3]。规则 LDPC 码的校验矩阵中不仅每一行中非零元素的个数是相同的,而且每一列中非零元素的个数也是相同的,而非规则LDPC码则不受到该条件的限制。下图给出的是一种规则LDPC码的校验矩阵。
4.部分源码
........................................................
Times = 500;%仿真模拟次数,值越大,效果越好,仿真时间越长
R = 0.5;%设置码率为1/2;
N = 192;%设置奇偶校验矩阵大小
M = N*R;
EbN0 = [0 1 2 3 4 5 6]; %设置Eb/N0;
Max_iter = 100; %最大迭代次数
H = func_Hgen(M,N);%产生奇偶校验矩阵
figure;
imshow(H,[]);title('奇偶校验均值H直观图');
for i=1:length(EbN0)
Bit_err(i) = 0; %设置误码率参数
Num_err = 0; %蒙特卡洛模拟次数
Numbers = 0; %误码率累加器
iter_moy_temp = [];%叠加寄存器
while Num_err <= Times
fprintf('Eb/N0 = %f\n', EbN0(i));
Num_err
Trans_data = round(rand(N-M,1)); %产生需要发送的随机数
[ldpc_code,newH] = func_Enc(Trans_data,H); %LDPC编码
u = [ldpc_code;Trans_data]; %LDPC编码
Trans_BPSK = 2*u-1; %BPSK
%通过高斯信道
N0 = 2*10^(-EbN0(i)/10);
Rec_BPSK = Trans_BPSK+sqrt(N0/2)*randn(size(Trans_BPSK));
%LDPC译码
[vhat,nb_iter] = func_Dec(Rec_BPSK,newH,N0,Max_iter);
iter_moy_temp(end+1) = nb_iter;
[nberr,rat]=biterr(vhat',u);
Num_err=Num_err+nberr;
Numbers=Numbers+1;
end
Bit_err(i) = Num_err/(N*Numbers);
end
.............................................................................
A152





































