1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWZlZ9q
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
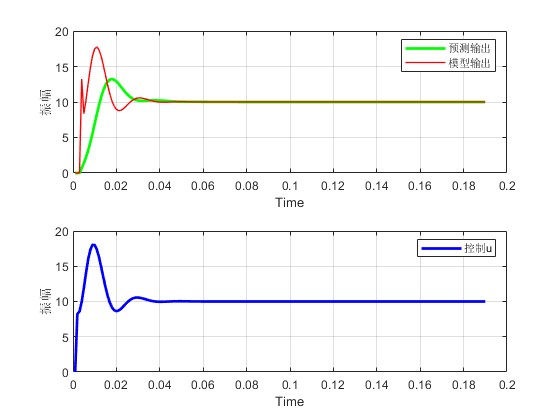
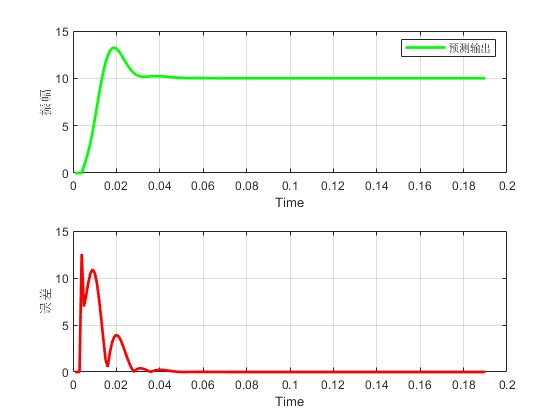
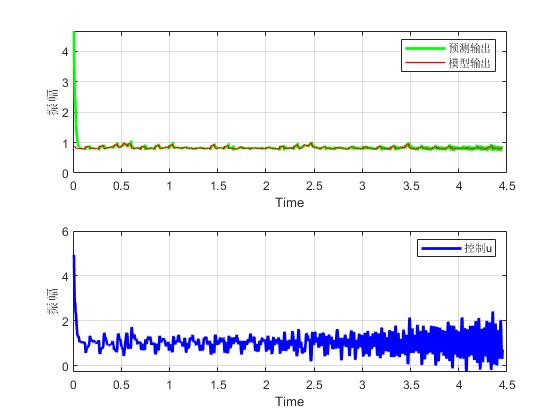
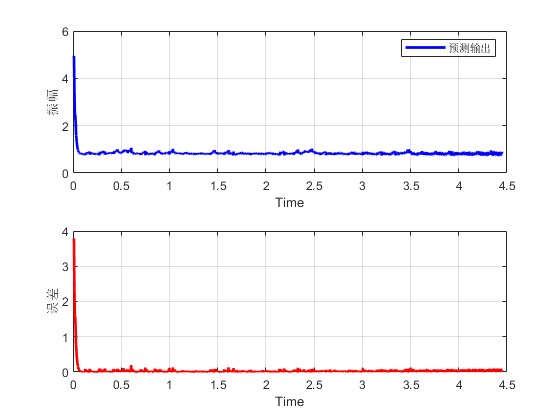
3.算法概述
在模型预测控制(MPC)中,控制信号的确定是通过在每个采样时刻输入序列为 时,最小化代价函数(2)。只有优化输入序列的第一个元素u(k)作为系统的输入,在下一个采样时刻k+1,新的优化问题是对于给定的优化控制问题而言的。在这种方法中,终止条件 可以看作是一个当时刻K+N趋于无穷时最小化代价函数的逼近器,但实际上更多的是用于保证闭环的稳定性。模型预测控制方法有一个非线性的缺点,且需要通过在每个采样时刻得到受约束的优化问题,同时需要通过在线计算来实现.
4.部分源码
...............................................................
%%
%参考轨迹
%参考轨迹
yr = zeros(ALL_Times,1);
yr = func_reference(ALL_Times,CV,OAT,ZT);
number1 = 25;
number2 = 16;
Set_Vlaue = 10;
yout_1 = 0;
cube_define;
%%
%循环仿真
%循环仿真3
for k=2:2*ALL_Times-10
if k <= ALL_Times%在线辨识学习
%控制器
[yout,Errs,u] = func_controller0(y_1,K,e,Set_Vlaue,u,A0,k,ALL_Times,number1,number2,CV(k),OAT(k),ZT(k));
...........................................................
%在线神经网络训练
%Inner network
for j=1:1:Nums
I(j) = State'*w1(:,j);
Iout(j) = 1/(1+exp(-I(j))); %隐含层
end
%Output of network
err_estimate(k) = w2'*Iout;
e1(k) = err_estimate(k)-e(k);
%Updata the weight
w2 = w2d1-(Learn_Rate*0.1*e1(k))*Iout+Alpha*(w2d1-w2d2);
for j=1:1:Nums
FI(j)=exp(-I(j))/(1+exp(-I(j)))^2;
end
%隐含层权值的更新
for i=1:1:Nums2
for j=1:1:Nums
dw1(i,j)=e1(k)*Learn_Rate*FI(j)*w2(j)*State(i);
end
end
%权值的更新
..........................................................
%开始实际的工作
Ind = k-ALL_Times+2;
%被控对象
yout(Ind) = func_system_model(y_1,u_1,CV(Ind),OAT(Ind),ZT(Ind));
%控制器输出
.................................................................
%辨识输出
..............................................
%延迟
%延迟
State(1) = yout(Ind);
State(2) = yout(Ind-1);
State(3) = u(Ind);
State(4) = u(Ind-1);
end
end
Start = 10;
Ends = length(yout)-10;
y_real = yout(Start:Ends);
y_pred = ym(Start:Ends);
y_pred1 = ym1(Start:Ends);
U_cont = u(Start:Ends);
Times = t(Start:Ends);
figure;
subplot(211);
plot(Times,y_pred,'g','linewidth',2);
hold on
plot(Times,y_real,'r','linewidth',1);
hold off
grid on
legend('预测输出','模型输出');
xlabel('Time')
ylabel('振幅')
subplot(212);
plot(Times,U_cont,'b','linewidth',2);
legend('控制u')
xlabel('Time')
ylabel('振幅')
grid on
figure;
subplot(211);
plot(Times,y_pred1,'b','linewidth',2);
legend('预测输出')
xlabel('Time')
ylabel('振幅')
grid on
subplot(212);
plot(Times,abs(y_real-y_pred),'r','linewidth',2);
xlabel('Time')
ylabel('误差')
grid on
Err = abs(mean(y_real(round(length(y_real)/2):end)-y_pred(round(length(y_pred)/2):end)));
disp('误差:');
Err
08_022_m





































