1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52bmpZq
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
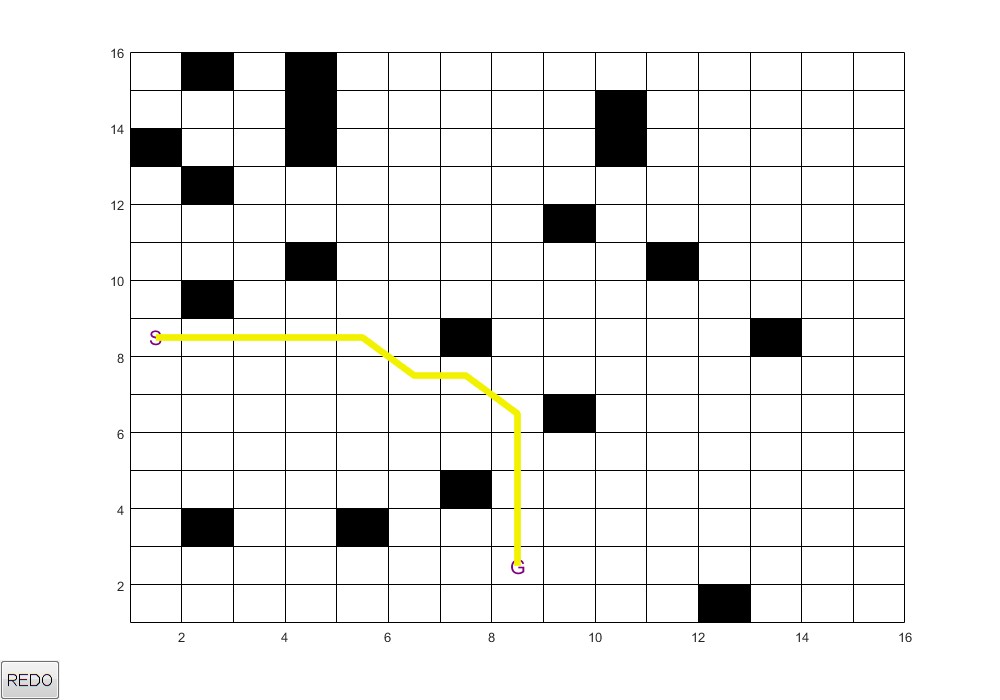
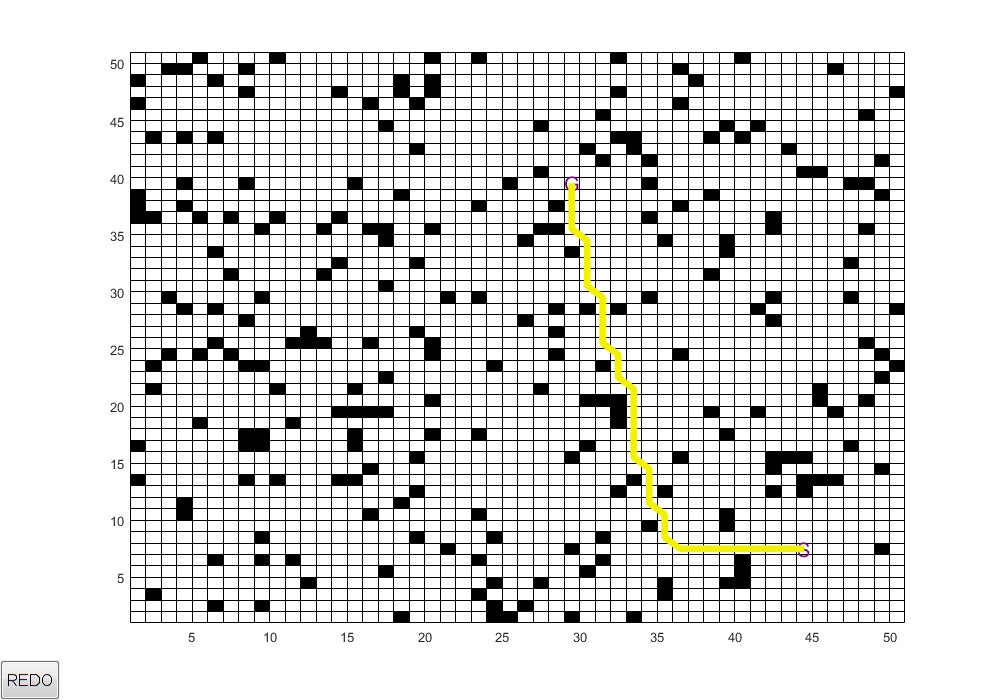
3.算法概述
Astar算法是一种图形搜索算法,常用于寻路。它是个以广度优先搜索为基础,集Dijkstra算法与最佳优先(best fit)算法特点于一身的一种 算法。它通过下面这个函数来计算每个节点的优先级,然后选择优先级最高的节点作为下一个待遍历的节点。
AStar(又称 A*),它结合了 Dijkstra 算法的节点信息(倾向于距离起点较近的节点)和贪心算法的最好优先搜索算法信息(倾向于距离目标较近的节点)。可以像 Dijkstra 算法一样保证找到最短路径,同时也像贪心最好优先搜索算法一样使用启发值对算法进行引导。简单点说,AStar的核心在于将游戏背景分为一个又一个格子,每个格子有自己的靠谱值,然后通过遍历起点的格子去找到周围靠谱的格子,接着继续遍历周围…… 最终找到终点。
4.部分源码
.......................................................
while ~max(ismember(setopen,goalposind))&&~isempty(setopen)
[temp,ii]=min(setopencosts+setopenheuristics);
[costs,heuristics,posinds]=findfvalue(setopen(ii),setopencosts(ii),field,goalposind);
setclose=[setclose;setopen(ii)];setclosecosts=[setclosecosts;setopencosts(ii)];
if ii>1&&ii<length(setopen)
setopen=[setopen(1:ii-1);setopen(ii+1:end)];
setopencosts=[setopencosts(1:ii-1);setopencosts(ii+1:end)];
setopenheuristics=[setopenheuristics(1:ii-1);setopenheuristics(ii+1:end)];
elseif 1==ii
setopen=[setopen(ii+1:end)];
setopencosts=[setopencosts(ii+1:end)];
setopenheuristics=[setopenheuristics(ii+1:end)];
else
setopen=[setopen(ii+1:end)];
setopencosts=[setopencosts(ii+1:end)];
setopenheuristics=[setopenheuristics(ii+1:end)];
end
for jj=1:length(posinds)
if ~isinf(costs(jj))
if ~max([setopen;setclose]==posinds(jj))
fieldpointers{posinds(jj)}=movementdirection(jj);
setopen = [setopen; posinds(jj)];
setopencosts = [setopencosts; costs(jj)];
setopenheuristics = [setopenheuristics; heuristics(jj)];
elseif max(setopen==posinds(jj))
i=find(setopen==posinds(jj));
if setopencosts(i)>costs(jj)
setopencosts(i)=costs(jj);
setopenheuristics(i)=heuristics(jj);
fieldpointers{setopen(i)}=movementdirection(jj);
end
else i=find(setclose==posinds(jj));
if setclosecosts(i)>costs(jj)
setclosecosts(i)=costs(jj);
fieldpointers{setclose(i)}=movementdirection(jj);
end
end
end
end
if isempty(setopen)
break;
end
end
if max(ismember(setopen,goalposind))
p=findwayback(goalposind,fieldpointers);
p=[p;inf*ones(2)];
for kk=1:length(p)
if p(kk+2,1)==inf||p(kk+1,1)==inf
break;
elseif abs(p(kk+2,1)-p(kk,1))==1&&abs(p(kk+2,2)-p(kk,2))==1
if p(kk+1,1)-p(kk,1)==1&&p(kk+2,2)-p(kk+1,2)==1
if field(p(kk,2)+1,p(kk,1))==inf
p;
else p=[p(1:kk,:);p(kk+2:end,:)];
end
elseif p(kk+1,2)-p(kk,2)==1&&p(kk+2,1)-p(kk+1,1)==1
if field(p(kk,2),p(kk,1)+1)==inf
p;
else p=[p(1:kk,:);p(kk+2:end,:)];
end
elseif p(kk+1,1)-p(kk,1)==-1&&p(kk+2,2)-p(kk+1,2)==1
if field(p(kk,2)+1,p(kk,1))==inf
p;
else p=[p(1:kk,:);p(kk+2:end,:)];
end
elseif p(kk+1,2)-p(kk,2)==1&&p(kk+2,1)-p(kk+1,1)==-1
if field(p(kk,2),p(kk,1)-1)==inf
p;
else p=[p(1:kk,:);p(kk+2:end,:)];
end
.................................................
end
end
else
p;
end
end
A171





































