1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52Zkphx
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
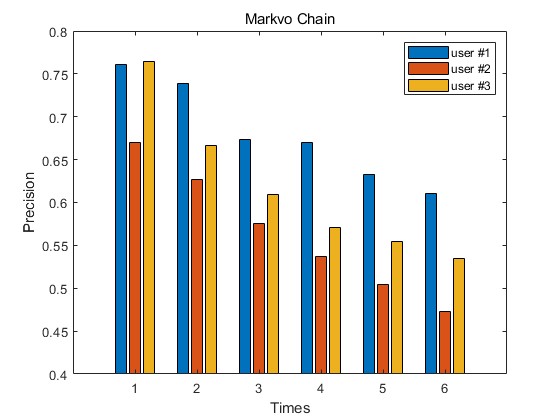
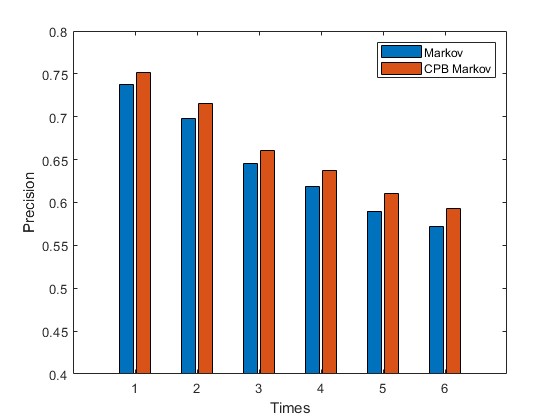
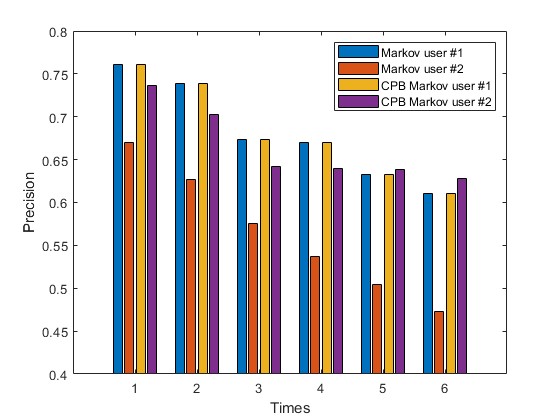
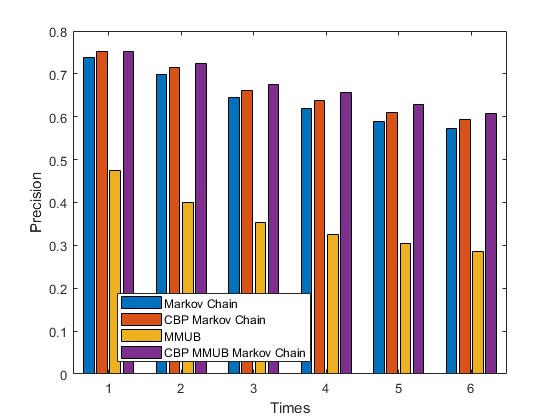
3.算法概述
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它用来描述一个含有隐含未知参数的马尔可夫过程。其难点是从可观察的参数中确定该过程的隐含参数。然后利用这些参数来作进一步的分析,例如模式识别。是在被建模的系统被认为是一个马尔可夫过程与未观测到的(隐藏的)的状态的统计马尔可夫模型。隐马尔可夫模型是马尔可夫链的一种,它的状态不能直接观察到,但能通过观测向量序列观察到,每个观测向量都是通过某些概率密度分布表现为各种状态,每一个观测向量是由一个具有相应概率密度分布的状态序列产生。所以,隐马尔可夫模型是一个双重随机过程----具有一定状态数的隐马尔可夫链和显示随机函数集。
4.部分源码
N1 = 100;%为了防止出现连续状态不变得情况,这里N1设置大点
N2 = 6;
N = N1 + N2; %前N1个用于训练,后N2个用于预测
Times = 1000;
%通过多次循环,计算正确率
for Nu = 1:length(Locaiton_id3)
UNo = Nu;%用户标号
for tim = 1:Times
UNo
tim
Dat = Locaiton_id3{1,UNo}(1+tim:N+tim);
State = unique(Dat);
%Counting the User Behavior Patterns
%Counting the User Behavior Patterns
Alpha = [];
maps = [];
MAP = [];
[Alpha,maps,MAP] = func_find_alpha_table(Dat,Locaiton_id3,State);
%Modeling the User Behaviors,the user’s behavior model can be built based on the resulting counting tables
%状态转移概率%释放概率
%对应算法步骤中计算STATE的步骤,计算moving or steady??
[seq,states] = func_cal_moving_steady(maps(1:N));%这里需要地址映射为自然数
[TRANS_EST,EMIS_EST] = hmmestimate(seq,states);
[r,c] = size(TRANS_EST);
for p1 = 1:r
for p2 = 1:c
if TRANS_EST(p1,p2) == 0
TRANS_EST(p1,p2) = eps;
end
if TRANS_EST(p1,p2) == 1
TRANS_EST(p1,p2) = 1-eps;
end
end
end
%通过vertiber算法计算概率
likelystates = hmmviterbi(seq,TRANS_EST,EMIS_EST);
Ps = length(find(likelystates==1))/N;
Pm = length(find(likelystates==2))/N;
%预测后面时刻的位置
likelihood_next_node = zeros(length(State),length(State));
for i = 1:length(State)
for j = 1:length(State)
if i == j
likelihood_next_node(i,j) = Ps*Alpha{i,j}(1);
else
likelihood_next_node(i,j) = Pm*Alpha{i,j}(1);
end
end
end
Plikelihood_next_node = zeros(length(State),N2);
for k = 1:N2
for i = 1:length(State)
Plikelihood_next_node(i,k) = likelihood_next_node(maps(N1-k+1),i)/(sum(likelihood_next_node(:,i))+eps);
end
[V,I] = max(Plikelihood_next_node(:,k));
for j = 1:size(MAP,1)
if I == MAP(j,2);
POS(k) = MAP(j,1);
end
end
end
NNN(:,tim) = (Dat(N1+1:N)==POS(1:N2)')';
end
for k = 1:N2
Precision1(k,Nu) = sum(NNN(k,:))/Times;
end
end
figure;
Views = [Precision1(:,1),Precision1(:,2),Precision1(:,3)];
bar(Views);
xlabel('Times');
ylabel('Precision');
legend('user #1','user #2','user #3');
title('MMUB');
figure;
Views = [mean(Precision1(:,:),2)];
bar(Views);
xlabel('Times');
ylabel('Precision');
legend('The average of 15 Users');
title('MMUB');
05_014_m





































