1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5mVlJZu
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
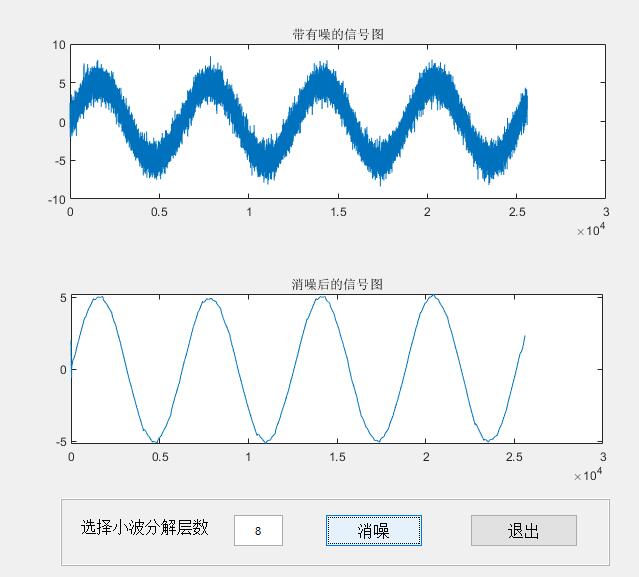
3.算法概述
近年来,小波理论得到了非常迅速的发展,而且由于其具备良好的时频特性,因而实际应用也非常广泛。在去噪领域中,小波理论也同样受到了许多学者的重视,他们应用小波进行去噪并获得了非常好的效果。
具体来说小波去噪方法的成功主要得益于小波变换具有如下特点:
(1)低熵性,小波系数的稀疏分布,使得图象变换后的熵降低;
(2)多分辨率,由于采用了多分辨率的方法,所以可以非常好地刻画信号的非平稳特征,如边缘、尖峰、断点等;
(3)去相关性,因为小波变换可以对信号进行去相关,且噪声在变换后有白化趋势,所以小波域比时域更利于去噪;
(4)选基灵活性,由于小波变换可以灵活选择变换基,从而对不同应用场合,对不同的研究对象,可以选用不同的小波母函数,以获得最佳的效果。
小波去噪方法包括三个基本的步骤:对含噪声信号进行小波变换;对变换得到的小波系数进行某种处理,以去除其中包含的噪声;对处理后的小波系数进行小波逆变换,得到去噪后的信号。小波去噪方法的不同之处集中在第一步。
4.部分源码
% 小波分解与程序,Xk0是要分解的原始信号,step是表示要分解的层数
[h0,h1,g0,g1]=filtercoefficience;
Xh=Xk0';D=0;
for lstep=1:step
N=length(Xh);
Yk=fft(Xh,N);
H0k=fft(h0,N);
H1k=fft(h1,N);
Xh=drawwing(ifft(Yk(1:N).*conj(H0k(1:N))));
Xh=real(Xh);D=real(D);
d=drawwing(ifft(Yk(1:N).*conj(H1k(1:N))));
thrd= ddencmp('den','wv',d);%用默阈值进行消噪处理
Td=abs(d)>thrd;
d=Td.*d;
D=[d,D];
end
%采用二项式正交小波滤波器
h0=[0.48296 0.83652 0.22414 -0.12941];%选用N为3的最小相位
N=length(h0);
for k=0:(N-1)
h1(k+1)=-(-1)^k*h0(N-k);
g0(k+1)=h0(N-k);
end
for t=0:(N-1)
g1(t+1)=h1(N-t);
end
A99





































