1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWalZ1v
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
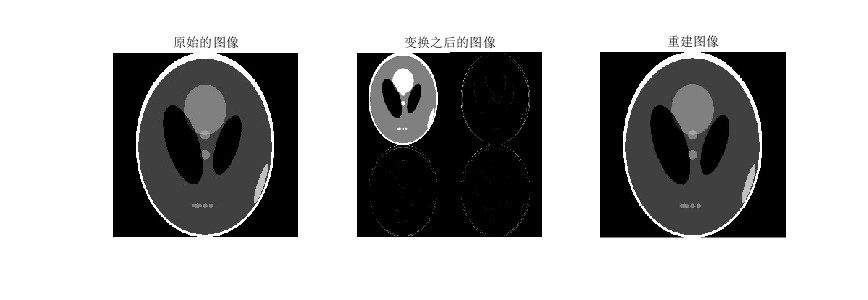
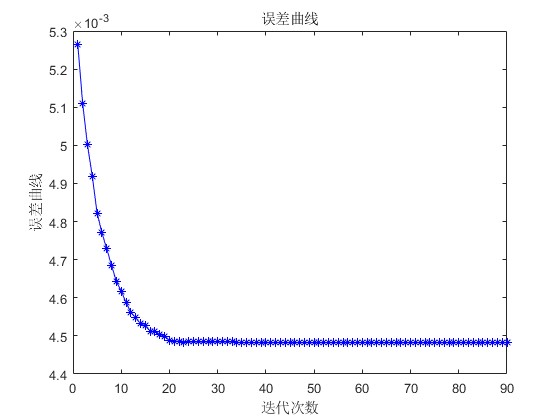
3.算法概述
PET测量数据(光子计数值)与生理模型紧密相关。然而,通常的重建方法多采用无生理意义的统计特性约束,从而忽略了反映生理特性的生理模型约束。本项目针对PET图像重建问题,提出利用H无穷粒子滤波混合算法融入数据统计特性模型、生理模型双重约束,并结合GPU完成重建过程的加速的方法。具体实现过程中以先验的共性生理特性作为约束,利用H无穷的鲁棒性处理不确定性,给出放射性药物浓度的粗估计,然后利用粒子滤波可以融合任何统计特性的能力,细调节估计值。以上迭代循环进行,最后给出放射性浓度分布与方差特性。由于采用了GPU加速策略,重建时间将显著缩短。该方法的实现将为PET图像重建提供新的技术手段。
4.部分源码
...........................................................
%读取PET图像
I = imread('shepp-logan.jpg');
N = 1;%分解级数
NUM = 90;%迭代次数
if isrgb(I) == 1
im = mat2gray(rgb2gray(I));
else
im = mat2gray(I);
end
im2 = im;
[r,c] = size(im2);
figure;
subplot(131);
imshow(im,[]);
title('原始的图像');
%得到行值与列值
[rows,cols]=size(im);
for i=1:N
%先对行进行一维快速分解
for j=1:cols/2^(i-1)
im(j,1:cols/2^(i-1)) = func_fast_wavelet_trans(im(j,1:cols/2^(i-1)),1);
end
%对列进行一维快速分解
for j=1:rows/2^(i-1)
im(1:rows/2^(i-1),j) = func_fast_wavelet_trans(im(1:rows/2^(i-1),j)',1);
end
end
%赋值给输出变量
im(abs(im)<0.1)=0;
subplot(132);
imshow(im)
title('变换之后的图像')
wl = im;
im_tmp = im;
%计算概率矩阵A
%计算概率矩阵A
%计算概率矩阵A
for jj = 1:NUM
im = im_tmp;
jj
% 进行重建
% 进行重建
for i=N:-1:1
for j=rows/2^(i-1):-1:1
im(1:rows/2^(i-1),j) = func_image_recon(im(1:rows/2^(i-1),j)',1,jj,im2(1:rows/2^(i-1),j)',wl(1:rows/2^(i-1),j)');
end
for j=cols/2^(i-1):-1:1
im(j,1:cols/2^(i-1)) = func_image_recon(im(j,1:cols/2^(i-1)),1,jj,im2(1:rows/2^(i-1),j)',wl(1:rows/2^(i-1),j)');
end
end
subplot(133);
imshow(im)
title('重建图像')
f0 = round(255*im);
f1 = round(255*im2);
errors(jj) = abs(sum(sum(f1 - f0)))/(8*256*256);
clear im
end
figure;
plot(1:NUM,errors,'b-*');
title('误差曲线');
xlabel('迭代次数');
ylabel('误差曲线');
09_023_m





































