1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWbmpdu
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
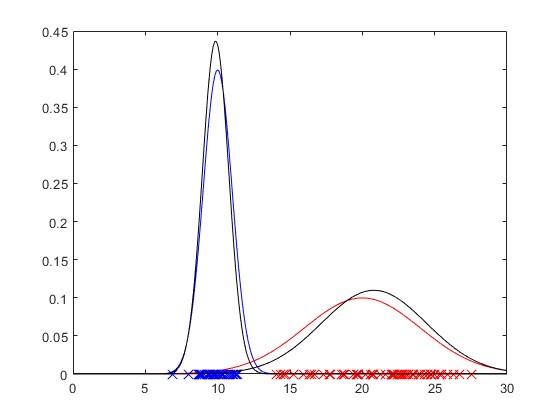
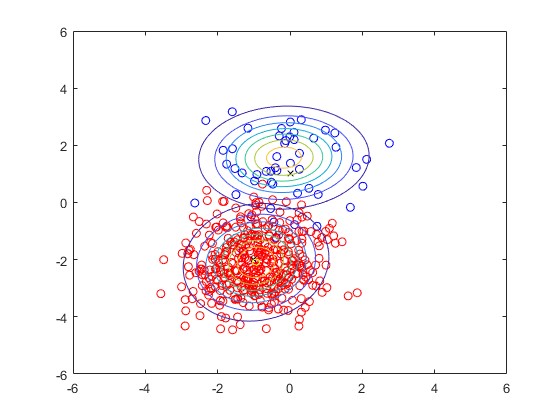
3.算法概述
EM (Expectation Maximization)算法是由Dempster、Laind和Rubin在1977年提出的一种求参数的极大似然估计方法,可以广泛地应用于处理缺损数据、截尾数据等带有噪声的不完整数据。针对不完整数据集,EM算法主要应用于以下两种情况的参数估计:第一,由于观测过程中本身的错误或局限性导致的观测数据自身不完整;第二,数据没有缺失,但是无法得到似然函数的解析解,或似然函数过于复杂,难以直接优化分析,而引入额外的缺失参数能使得简化后的似然函数便于参数估计。
4.部分源码
.................................................................
z1 = gaussian2D(gridX, mu1, sigma1);
z2 = gaussian2D(gridX, mu2, sigma2);
Z1 = reshape(z1, gridSize, gridSize);
Z2 = reshape(z2, gridSize, gridSize);
[C, h] = contour(u, u, Z1);
[C, h] = contour(u, u, Z2);
axis([-6 6 -6 6])
title('Original Data and PDFs');
m = size(X, 1);
k = 2;
n = 2;
indeces = randperm(m);
mu = X(indeces(1:k), :);
sigma = [];
for (j = 1 : k)
sigma{j} = cov(X);
end
phi = ones(1, k) * (1 / k);
%Run Expectation Maximization
W = zeros(m, k);
for (iter = 1:1000)
%Expectation
pdf = zeros(m, k);
for (j = 1 : k)
pdf(:, j) = gaussian2D(X, mu(j, :), sigma{j});
end
pdf_w = bsxfun(@times, pdf, phi);
W = bsxfun(@rdivide, pdf_w, sum(pdf_w, 2));
%Maximization
prevMu = mu;
for (j = 1 : k)
phi(j) = mean(W(:, j), 1);
mu(j, :) = weightedAverage(W(:, j), X);
sigma_k = zeros(n, n);
Xm = bsxfun(@minus, X, mu(j, :));
for (i = 1 : m)
sigma_k = sigma_k + (W(i, j) .* (Xm(i, :)' * Xm(i, :)));
end
sigma{j} = sigma_k ./ sum(W(:, j));
end
if (mu == prevMu)
break
end
end
figure(2);
hold off;
plot(X1(:, 1), X1(:, 2), 'bo');
hold on;
plot(X2(:, 1), X2(:, 2), 'ro');
.....................................................
A436





































