1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qalppt
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
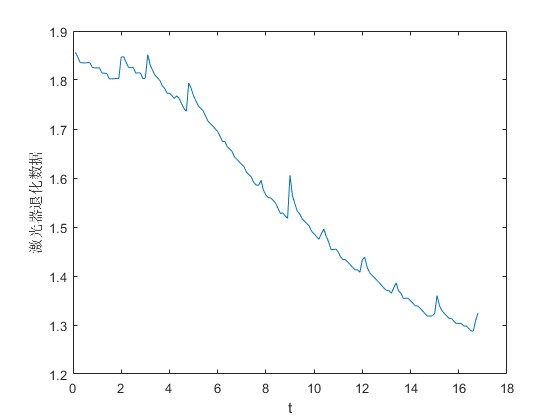
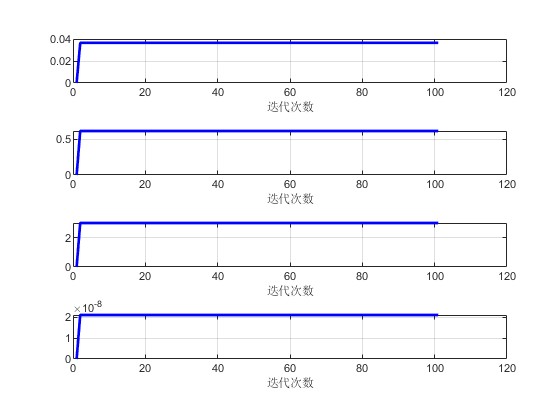
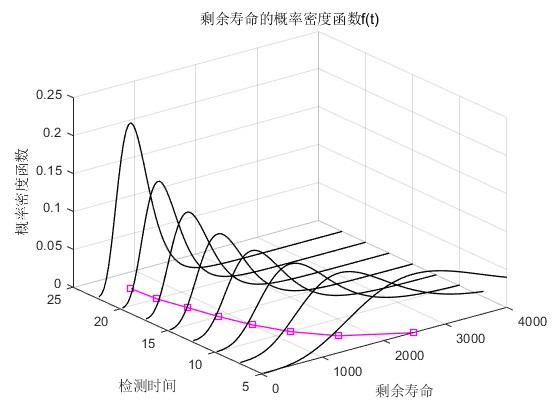
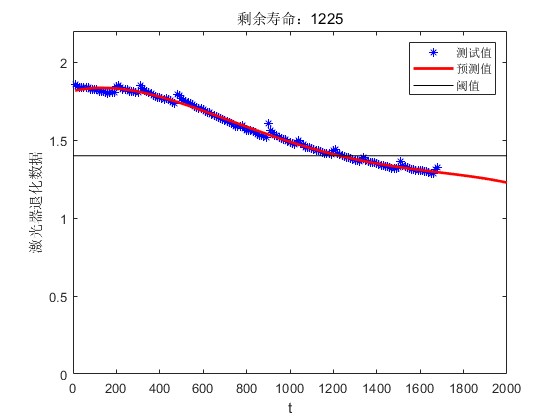
3.算法概述
伽马过程(Gamma Process)是随机过程理论中一类重要过程Lévy过程的一种,其增量服从独立的gamma分布,可以用于描述单调递增的变化过程,属于Lévy subordinator中的一种,gamma过程,通常记作,由两个正参数决定,其中称为形状参数,控制了跳跃点到达的频率,称为尺度参数,控制了跳跃的跃度。同时,该过程假设在时刻t=0时,其值为0,即在初始时刻位置在原点。
使用伽马函数定义了许多概率分布,例如伽马分布,Beta分布,狄利克雷分布,卡方分布和学生t分布等。 对于数据科学家,机器学习工程师,研究人员来说,伽马函数可能是一种最广泛使用的函数,因为它已在许多分布中使用。然后将这些分布用于贝叶斯推理,随机过程(例如排队模型),生成统计模型(例如潜在狄利克雷分配)和变分推理。
4.部分源码
............................................................
for i = 1:Iter
i
ykt = yk;
ykt1 = [0,yk(1:end-1)];
xkt = xk;
xkt1 = [0,xk(1:end-1)];
%粒子滤波
if i == 1
[Exk,Ws] = func_Particlefilter(ykt,xkt,c0,delta0);
[Exk1,Ws] = func_Particlefilter(xkt1,ykt1,c0,delta0);
[Exklog,Ws]= func_Particlefilter(log(xk_xk1),ykt1,c0,delta0);
else
[Exk,Ws] = func_Particlefilter(ykt,xkt,c_(i-1),delta_(i-1));
[Exk1,Ws] = func_Particlefilter(xkt1,ykt1,c_(i-1),delta_(i-1));
[Exklog,Ws]= func_Particlefilter(log(xk_xk1),log(ykt1),c_(i-1),delta_(i-1));
end
%E步骤
if i == 1
E1 = sum(a0*dt*log(epls0) - log(gamma(a0*dt))+(a0*dt-1)*Exklog-epls0*(Exk-Exk1));
E2 = sum(-log(delta0)-0.5*log(2*pi)-1/(2*delta0^2)*(yk.^2-2*yk.*c0.*Exk+c0^2.*Exk.^2));
theta = E1+E2;
else
E1 = sum(a_(i)*dt*log(epls_(i)) - log(gamma(a_(i)*dt))+(a_(i)*dt-1)*mean(log(xk_xk1))-epls_(i)*(Exk-Exk1));
E2 = sum(-log(delta_(i-1))-0.5*log(2*pi)-1/(2*delta_(i-1)^2)*(yk.^2-2*yk.*c_(i-1).*Exk+c_(i-1)^2.*Exk.^2));
theta = E1+E2;
end
%M步骤
if i == 1
a = Exk(end)/t(end);
epls = a*t(end)/max(Exk(end),1);
else
a = Exk(end)/t(end);
epls = a*t(end)/max(Exk(end),1);
end
c = sum(yk.*Exk)./sum(Exk.^2);
delta = sqrt(1/n*sum(yk.^2 - 2*yk.*c.*Exk + c^2.*Exk.^2));
a_(i+1) = a;
epls_(i+1) = epls;
c_(i+1) = c;
delta_(i+1)= delta;
end
................................................
figure;
idx=0;
for jj = sers
idx=idx+1;
a_s = jj*a_;
for j = 1:length(tr)
F_tmps = [];
for s = 1:length(xc)
F_tmps(s) = func_gamma(xc(s),a_s(end)*tr(j),(D-xc(s))/epls_(end))/gamma(a_s(end)*tr(j));
end
F(j) = mean(F_tmps)/(sers(end)-jj)^0.5;
end
f=abs(F);
plot3(400*tr,(jj)*ones(size(tr)),f,'k','linewidth',1);
[V,I] = max(f);
hold on
xx(idx) = 400*tr(I);
yy(idx) = (jj);
ff{idx} = f;
end
plot3(xx(1:end-1),yy(1:end-1),0*ones(size(xx(1:end-1))),'m-s','linewidth',1);
xlabel('剩余寿命');
ylabel('检测时间');
zlabel('概率密度函数');
title('剩余寿命的概率密度函数f(t)');
grid on
01_187m





































