1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWTkp5y
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
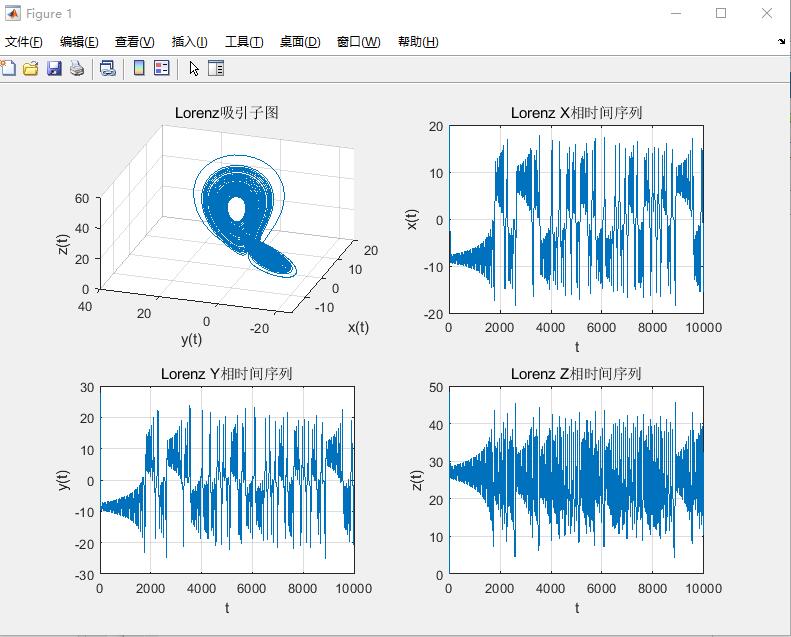
3.算法概述
Lorenz发现了第一个混沌吸引子——Lorenz系统,从此揭开了混沌研究的序幕,该系统也称为Lorenz混沌系统。从此,人们不断发现新的混沌奇异性,不断地加深与统一对混沌的理解。Lorenz系统是数值试验中最早发现的呈现混沌运动的耗散系统。
4.部分源码
...............................................................
for i=1:Number-1
K1=p*(y(i)-x(i));
L1=r*x(i)-y(i)-x(i)*z(i);
M1=-b*z(i)+x(i)*y(i);
K2=p*((y(i)+h/2*L1)-(x(i)+h/2*K1));
L2=r*(x(i)+h/2*K1)-(y(i)+h/2*L1)-(x(i)+h/2*K1)*(z(i)+h/2*M1);
M2=-b*(z(i)+h/2*M1)+(x(i)+h/2*K1)*(y(i)+h/2*L1);
K3=p*((y(i)+h/2*L2)-(x(i)+h/2*K1));
L3=r*(x(i)+h/2*K1)-(y(i)+h/2*L2)-(x(i)+h/2*K1)*(z(i)+h/2*M2);
M3=-b*(z(i)+h/2*M1)+(x(i)+h/2*K1)*(y(i)+h/2*L2);
K4=p*((y(i)+h*L3)-(x(i)+h*K3));
L4=r*(x(i)+h*K3)-(y(i)+h*L3)-(x(i)+h*K3)*(z(i)+h*M3);
M4=-b*(z(i)+h*M3)+(x(i)+h*K3)*(y(i)+h*L3);
x(i+1)=x(i)+h/6*(K1+2*K2+2*K3+K4);
y(i+1)=y(i)+h/6*(L1+2*L2+2*L3+L4);
z(i+1)=z(i)+h/6*(M1+2*M2+2*M3+M4);
end
figure(1);
subplot(221);
plot3(x,y,z);
xlabel('x(t)');
ylabel('y(t)');
zlabel('z(t)');
title('Lorenz吸引子图');
grid on;
view([-72,40]);
subplot(222);
plot(x);
xlabel('t');
ylabel('x(t)');
title('Lorenz X相时间序列');
grid on;
subplot(223);
plot(y);
xlabel('t');
ylabel('y(t)');
title('Lorenz Y相时间序列');
grid on;
subplot(224);
plot(z);
xlabel('t');
ylabel('z(t)');
title('Lorenz Z相时间序列');
grid on;
A351





































