1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJeZlptx
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览


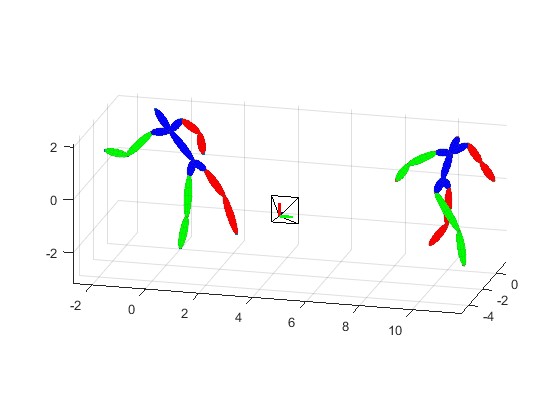
3.算法概述
三维姿态估计是计算机视觉领域中一个非常重要的问题,它在许多应用中都具有重要的作用,如人机交互、姿态识别、动作捕捉等。在过去的几年中,随着深度学习技术的发展,基于深度学习的方法取得了很大的进展,但是这些方法仍然存在许多问题,如对于遮挡和复杂姿态的处理等。
4.部分源码
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
rng('default')
%FPGA/MATLAB/simulink仿真
%微信公众号:matworld
%初始spread
mu = 1;
%根据遗传算法进行参数的拟合
MAXGEN = 20;
NIND = 50;
Chrom = crtbp(NIND,1*10);
%14个变量的区间
Areas = [0.5;
1.5];
FieldD = [rep([10],[1,1]);Areas;rep([0;0;0;0],[1,1])];
LR = zeros(NIND,1);
MU2 = zeros(MAXGEN,1);
gen = 0;
for a=1:1:NIND
a
LR(a) = mu;
%计算对应的目标值
errs = func_obj(LR(a));
E = errs;
J(a,1) = E;
end
Objv = (J+eps);
gen = 0;
while gen < MAXGEN;
gen
P1 = 0.9;
P2 = 1-P1;
FitnV=ranking(Objv);
Selch=select('sus',Chrom,FitnV);
Selch=recombin('xovsp', Selch,P1);
Selch=mut( Selch,P2);
phen1=bs2rv(Selch,FieldD);
for a=1:1:NIND
if gen == 1
LR(a) = mu;
else
LR(a) = phen1(a,1);
end
%计算对应的目标值
errs = func_obj(LR(a));
E = errs;
JJ(a,1) = E;
end
Objvsel=(JJ+eps);
[Chrom,Objv]=reins(Chrom,Selch,1,1,Objv,Objvsel);
gen=gen+1;
%保存参数收敛过程和误差收敛过程以及函数值拟合结论
MU2(gen) = mean(LR);
Error(gen) = mean(JJ);
deltaf = Error(gen);
end
MU_best = MU2(end);
MU_best
save best_mu.mat MU_best
% figure;
% plot(MU2(3:end),'b-o');
% xlabel('Iteration Number');
% ylabel('mu');
% grid on;
function vis3Dskel(shapes,skels,viewpoint,flagShowCam,mode,Num,N)
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
switch lower(mode)
case 'ellipse'
limbRadius = 0.15;
limbColour = 0.7*ones(1,3);
M = repmat(limbColour,length(indices),1);
shape(1,:)=shape(1,:)+(jj-1)*10;
plot3(shape(1,:),shape(3,:),shape(2,:),'.'); %,控制15个点的。。可以改为plot3(shape(1,:),shape(3,:),shape(2,:),'k.','MarkerSize',50); 'R.','MarkerSize',30,关节点状态,红色30大小。
hold on
grid on
for i = 1:length(indices)
P1 = [shape(1,I(i)) shape(3,I(i)) shape(2,I(i))];
P2 = [shape(1,J(i)) shape(3,J(i)) shape(2,J(i))];
P = 0.5*(P1 + P2);
U = [ null(P1 - P2)'; (P1 -P2)/norm(P1-P2)]; % 函数null用来求解零空间,即满足方程组A*X=0的解空间。实际上是求出解空间的一组解(基础解系)。
% 语法:z=null(A),z的列向量为方程组的正交规范基,满足z‘ x z=I。
% null(A)给出的是矩阵A的null space的单位正交基。对于矩阵A,用null(A)命令就直接求出来AX=0的解
S = eye(3); S(1,1) = 1.5*norm(P1-P2);
l = 0.55*norm(P1-P2);
[x,y,z] = ellipsoid(0,0,0,limbRadius,limbRadius,l,8);
axis equal;
xv =x(:);
yv = y(:);
zv = z(:);
newXYZ = U'*[xv';yv';zv'];
xnew = reshape(newXYZ(1,:)+P(1),size(x,1),size(x,2));
ynew = reshape(newXYZ(2,:)+P(2),size(x,1),size(x,2));
znew = reshape(newXYZ(3,:)+P(3),size(x,1),size(x,2));
handle = patch(surf2patch(xnew,ynew,znew));
set(handle,'EdgeColor',[0.3 0.3 0.3],'EdgeAlpha',0.1);
set(handle,'FaceLighting','phong','AmbientStrength',0.6);
set(handle,'FaceColor', skel.tree(I(i)).color);
set(handle,'BackfaceLighting','lit');
end
case 'stick'
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
end
09_051_m
---





































