1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJeUmpZy
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
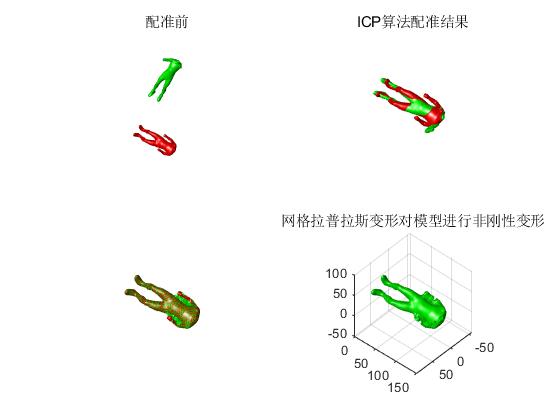
2.部分仿真图预览
3.算法概述
ICP算法是当前应用最广的点云配准算法。ICP算法虽然基本能够满足点云配准在精度上的要求,但算法本身计算效率不高,花费时间太多,特别 是对于实际测量中的海量数据无法直接使用。因此 需要对其进行改进,提高计算效率。ICP算法的时间代价是O(NPNX)。在实际测量 中,当数据量很大时(例如几十万甚至几百万个点), 所花费的时间将是惊人的。如果能够减少时间代价到O(NP),并且同时保证配准精度的话,就能应用于 实际测量的模型之中。由于ICP算法中主要是求最 近点集的算法花费时间比较多,如果能够把这个步骤 的时间代价减少到O(NP),即可达到目的。然后利用k-dtree寻找这些特征点在参考点云 中的最近点,通过这些步骤可以减少算法的时间代价.
4.部分源码
.......................................................
[Datasetsource0,Datasettarget0]=func_sel_same_nums(target,source);
if ISICP == 2
targetV = target;
sourceV = Reallignedsource;
targetF = ftarget;
sourceF = fsource;
Iter = 10;
tic;
%拉普拉斯算法部分,可以通过多次运行,修复错误的部分
[targetF,targetV,sourceF,sourceV,errors1] = func_Laplacian3Dmesh(targetV,sourceV,targetF,sourceF,Iter);
errors = sort([errors1],'descend');
dt2 = toc;
figure(1);
subplot(223);
trisurf(targetF,targetV(:,1),targetV(:,2),targetV(:,3),'facecolor','r','Edgecolor','none');
axis off;
hold on
lighting phong;
set(gca,'DataAspectRatio',[1 1 1],'PlotBoxAspectRatio',[1 1 1]);
trisurf(sourceF,sourceV(:,1),sourceV(:,2),sourceV(:,3),'facecolor','g','Edgecolor','none');
light
view([132,42]);
figure(1);
subplot(224);
trisurf(sourceF,sourceV(:,1),sourceV(:,2),sourceV(:,3),'facecolor','g','Edgecolor','none');
light
title('网格拉普拉斯变形对模型进行非刚性变形');
lighting phong;
set(gca,'DataAspectRatio',[1 1 1],'PlotBoxAspectRatio',[1 1 1]);
view([132,42]);
figure(3);
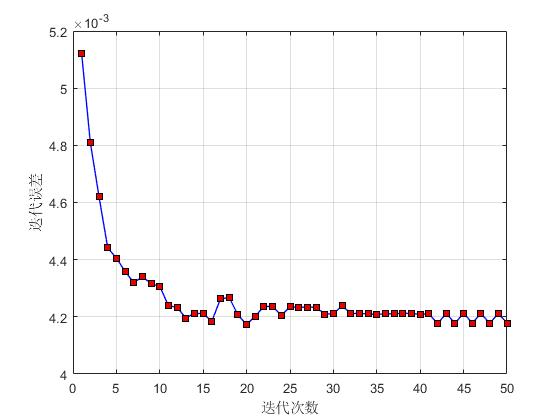
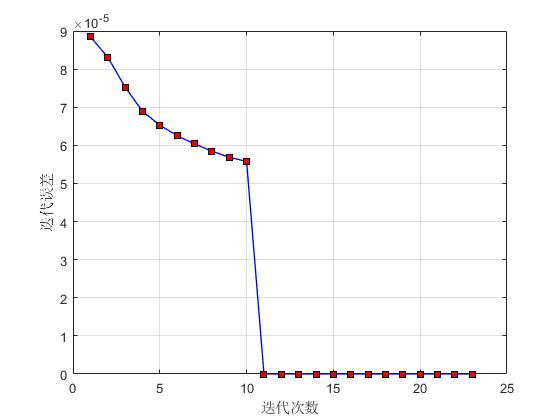
plot(errors,'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('迭代次数');
ylabel('迭代误差');
grid on
end
09_047_m





































