1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56bm51t
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
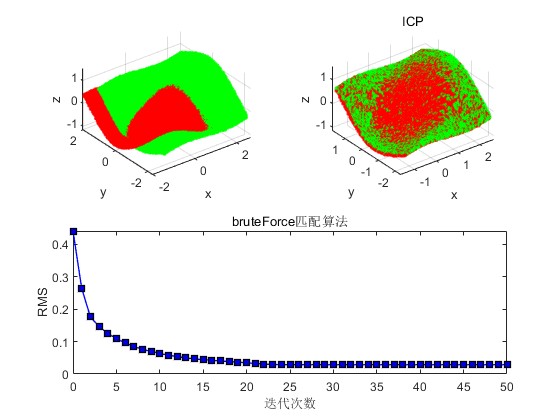
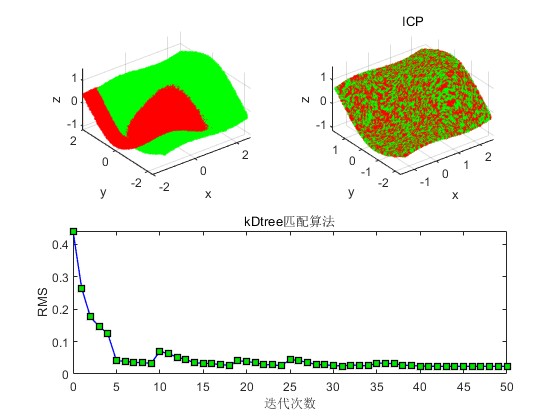
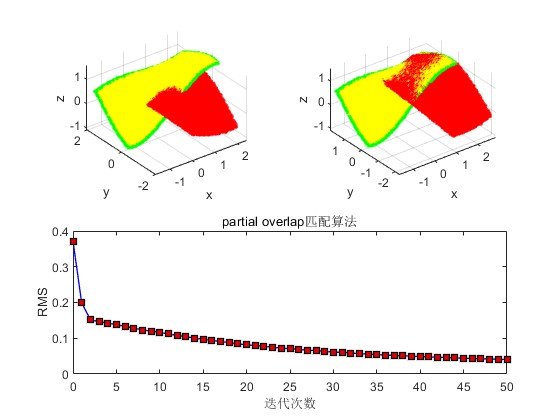
3.算法概述
ICP算法能够使不同的坐标下的点云数据合并到同一个坐标系统中,首先是找到一个可用的变换,配准操作实际是要找到从坐标系1到坐标系2的一个刚性变换。ICP算法本质上是基于最小二乘法的最优配准方法。该算法重复进行选择对应关系点对, 计算最优刚体变换,直到满足正确配准的收敛精度要求。ICP 算法的目的是要找到待配准点云数据与参考云数据之间的旋转参数R和平移参数 T,使得两点数据之间满足某种度量准则下的最优匹配。
假设给两个三维点集 X1 和 X2,ICP方法的配准步骤如下:
第一步,计算X2中的每一个点在X1 点集中的对应近点;
第二步,求得使上述对应点对平均距离最小的刚体变换,求得平移参数和旋转参数;
第三步,对X2使用上一步求得的平移和旋转参数,得到新的变换点集;
第四步, 如果新的变换点集与参考点集满足两点集的平均距离小于某一给定阈值,则停止迭代计算,否则新的变换点集作为新的X2继续迭代,直到达到目标函数的要求。
4.部分源码
................................................................................
% If Matching == 'Delaunay', a triangulation is needed
if strcmp(arg.Matching, 'Delaunay')
DT = DelaunayTri(transpose(q));
end
% If Matching == 'kDtree', a kD tree should be built (req. Stat. TB >= 7.3)
if strcmp(arg.Matching, 'kDtree')
kdOBJ = KDTreeSearcher(transpose(q));
end
% If edge vertices should be rejected, find edge vertices
if arg.EdgeRejection
if isempty(arg.Boundary)
bdr = find_bound(q, arg.Triangulation);
else
bdr = arg.Boundary;
end
end
if arg.Extrapolation
% Initialize total transform vector (quaternion ; translation vec.)
qq = [ones(1,arg.iter+1);zeros(6,arg.iter+1)];
% Allocate vector for direction change and change angle.
dq = zeros(7,arg.iter+1);
theta = zeros(1,arg.iter+1);
end
t(1) = toc;
% Go into main iteration loop
for k=1:arg.iter
% Do matching
switch arg.Matching
case 'bruteForce'
[match mindist] = match_bruteForce(q,pt);
case 'Delaunay'
[match mindist] = match_Delaunay(q,pt,DT);
case 'kDtree'
[match mindist] = match_kDtree(q,pt,kdOBJ);
end
.......................................................................
% Add to the total transformation
TR(:,:,k+1) = R*TR(:,:,k);
TT(:,:,k+1) = R*TT(:,:,k)+T;
% Apply last transformation
pt = TR(:,:,k+1) * p + repmat(TT(:,:,k+1), 1, Np);
% Root mean of objective function
ER(k+1) = rms_error(q(:,q_idx), pt(:,p_idx));
% If Extrapolation, we might be able to move quicker
if arg.Extrapolation
qq(:,k+1) = [rmat2quat(TR(:,:,k+1));TT(:,:,k+1)];
dq(:,k+1) = qq(:,k+1) - qq(:,k);
theta(k+1) = (180/pi)*acos(dot(dq(:,k),dq(:,k+1))/(norm(dq(:,k))*norm(dq(:,k+1))));
if arg.Verbose
disp(['Direction change ' num2str(theta(k+1)) ' degree in iteration ' num2str(k)]);
end
if k>2 && theta(k+1) < 10 && theta(k) < 10
d = [ER(k+1), ER(k), ER(k-1)];
v = [0, -norm(dq(:,k+1)), -norm(dq(:,k))-norm(dq(:,k+1))];
vmax = 25 * norm(dq(:,k+1));
dv = extrapolate(v,d,vmax);
if dv ~= 0
q_mark = qq(:,k+1) + dv * dq(:,k+1)/norm(dq(:,k+1));
q_mark(1:4) = q_mark(1:4)/norm(q_mark(1:4));
qq(:,k+1) = q_mark;
TR(:,:,k+1) = quat2rmat(qq(1:4,k+1));
TT(:,:,k+1) = qq(5:7,k+1);
% Reapply total transformation
pt = TR(:,:,k+1) * p + repmat(TT(:,:,k+1), 1, Np);
% Recalculate root mean of objective function
% Note this is costly and only for fun!
switch arg.Matching
case 'bruteForce'
[~, mindist] = match_bruteForce(q,pt);
case 'Delaunay'
[~, mindist] = match_Delaunay(q,pt,DT);
case 'kDtree'
[~, mindist] = match_kDtree(q,pt,kdOBJ);
end
ER(k+1) = sqrt(sum(mindist.^2)/length(mindist));
end
end
end
t(k+1) = toc;
end
if not(arg.ReturnAll)
TR = TR(:,:,end);
TT = TT(:,:,end);
end
A344





































