1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Yk5tt
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
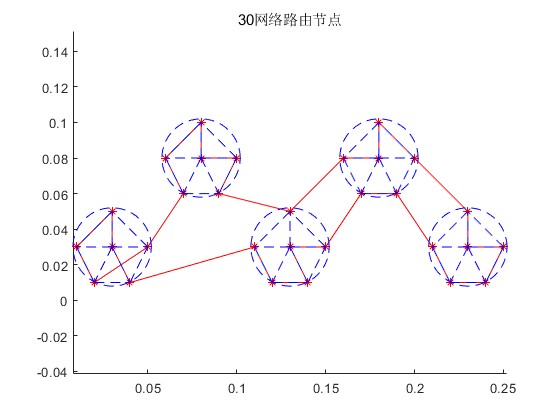
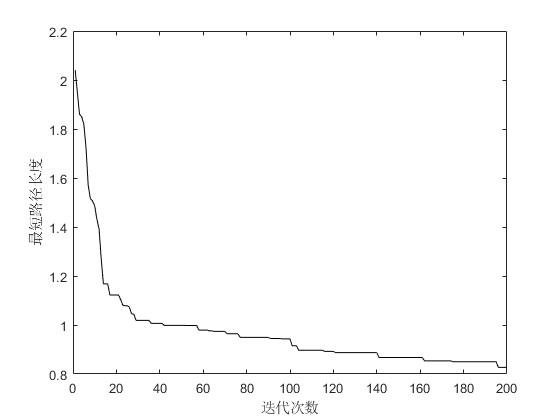
3.算法概述
step1. 当有连接请求时,算法开始,考察源节点S是否为域的边界节点,不是的话在域内使用最短跳算法路由至此域的边界节点
域的边界节点用U表示(图中A, B),下一跳接口为[D, N, r(U, N)],D为宿节点,N为下一跳结点,r(U, N) = {wU, wN, hU-N},wU, wN为U,N结点间波长,hU-N 是U,N间的代价,再到下一跳r(N, E),E为下一个域的边界节点。
step2. 根据OSPF 协议规范,在请求连接的两点之间,用Dijkstra 算法计算出所有路径,尽量消除冗余存储和冗余计算,挑选出代价最少的路径,hU-D = hU-N+ hN-E + …+h*-D, 总代价为各跳路径相加,
step3. 考察波长连续性,: r(U, N) = {wU, wN1, hU-N}, r(N, E) = {wN2, wE1, hN-E}…r(*, D) = {w*2, wD, h*-D}.
If wN1 = wN2, && wE1= wE2 &&…. w*1= w*2, return null,
否则,加入波长变换器, 此路径代价变为C。
step4. 考察次短路径,是否存在符合波长连续性的波长,若有,则转到步骤7,否则执行步骤6;
step5. 设最短路径增加波长变换器代价为C,采用次短路径的代价为H2,比较C、H2,若C<H2,则采用增加波长变换器方法,选择最短路径,否则采用次短路径;跳至步骤4;
step6. 循环执行步骤4,5,直至计算出合适的路径;
Step7. 显示所选路径,算法结束,S结点开始发包至宿节点D
4.部分源码
........................................................................
[D,M]=tsp(webpoint);
popsize=100;
N=200; %N为迭代次数
pcro=0.85;
pmut=0.5;
gen=1;
minval=inf;
pop=initialize(popsize,webpoint);
while gen<=N
gen
val=adapt(pop,popsize,webpoint,D);
fitval=(1000./val).^15;
[valmin,minind]=min(val);
%保存最优
if valmin<minval
minval=valmin;
minpath=pop(minind,:);
end
minf(gen)=minval; %最短路径长度
pop=select(pop,fitval,popsize,webpoint,minpath); %比例选择
pop=crossover(pop,pcro,popsize,webpoint); %OX交叉
pop=mutation(pop,pmut,popsize,webpoint); %变异
drawTSP(M,minpath,minval,gen,0);
gen=gen+1;
end
drawTSP(M,minpath,minval,gen,1);
hold on
...................................................................
axis equal
12_001_m





































