1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56blJ9t
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
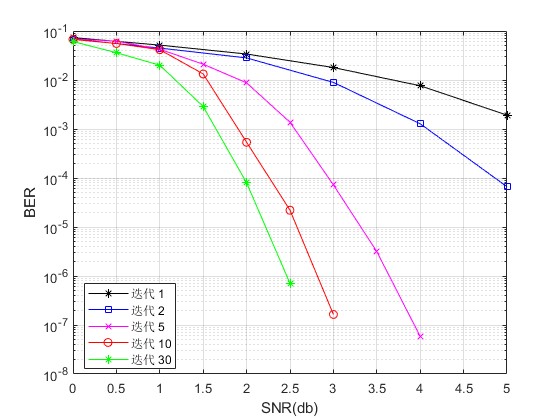
3.算法概述
LDPC仿真系统图LDPC 码的奇偶校验矩阵H是一个稀疏矩阵,相对于行与列的长度,校验矩阵每行、列中非零元素的数目(我们习惯称作行重、列重)非常小,这也是LDPC码之所以称为低密度码的原因。由于校验矩阵H的稀疏性以及构造时所使用的不同规则,使得不同LDPC码的编码二分图(Taner图)具有不同的闭合环路分布。而二分图中闭合环路是影响LDPC码性能的重要因素,它使得LDPC码在类似可信度传播(Belief ProPagation)算法的一类迭代译码算法下,表现出完全不同的译码性能。当H的行重和列重保持不变或尽可能的保持均匀时,我们称这样的LDPC码为正则LDPC码,反之如果列、行重变化差异较大时,称为非正则的LDPC码。研究结果表明正确设计的非正则LDPC码的性能要优于正则LDPC。根据校验矩阵H中的元素是属于GF(2)还是GF(q)(q=2p),我们还可以将LDPC码分为二元域或多元域的LDPC码。研究表明多元域LDPC码的性能要比二元域的好。
4.部分源码
clc;
clear;
close all;
warning off;
addpath(genpath(pwd));
global inters;
inters= 2;
%%
%参数的初始化
q = 127;
M = 5*q; %矩阵行数
N = 10*q;%矩阵列数
a = 2;
b = 7;
%QC构造稀疏矩阵
H = func_QC_H(a,b,q,M,N);
%将系数矩阵转换为生成矩阵
[G,valid] = func_H2G(H);
[N1,N2] = size(G);
%仿真信噪比,迭代次数少的时候,可以增加信噪比的仿真长度区间
NoisedB = [0:1:5];
LL = [200,150,100,50,30,20,15,10,10,10]*4;
All_frame = N2;
for i = 1 : length(NoisedB)
Num_err = 0;
xx = 10^(NoisedB(i)/10);
sigma = 1/sqrt(xx);
idx = 0;
while Num_err<LL(i)
[Num_err,i]
idx= idx+1;
%产生随机数据作为测试数据
x = (sign(randn(1,size(G,1)))+1)/2;
%LDPC编码
y = mod(x*G,2);
%BPSK映射
z = 2*y-1;
%加入噪声
z = awgn(z,NoisedB(i),'measured');
%LDPC译码
z_hat = func_Ldpc_dec(z,sigma,H);
x_hat = z_hat(M+1:N);
x_hat1= x_hat';
%误码率统计
Num_err = Num_err + sum(xor(x,x_hat1));
end
BER1(i) = Num_err/All_frame/idx;
end
figure;
semilogy(NoisedB,BER1,'r-*');
grid on
xlabel('SNR(db)');
ylabel('BER');
legend('QC-LDPC');
if inters==1
save QC1.mat NoisedB BER1
end
if inters==2
save QC2.mat NoisedB BER1
end
if inters==5
save QC5.mat NoisedB BER1
end
if inters==10
save QC10.mat NoisedB BER1
end
if inters==30
save QC30.mat NoisedB BER1
end
14_007_m





































