1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJucl5Zs
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
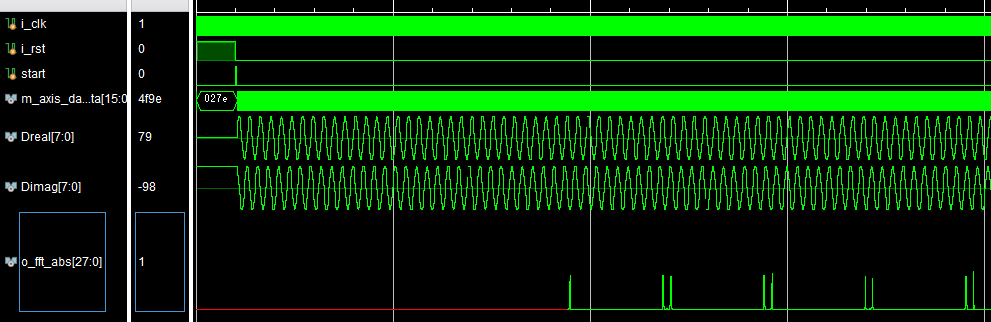
3.算法概述
FFT是一种高效的计算傅里叶变换的算法,可以降低傅里叶变换的计算复杂度。对于长度为$N=2^m$的信号序列,其中$m$是整数,快速傅里叶变换可以通过分治法和蝶形运算来实现。其中,分治法将信号分为两个子序列,分别进行傅里叶变换,然后通过蝶形运算组合子序列的结果。256点FFT是指将长度为256的时域信号序列转换为频域表示的过程。对于256点FFT,信号序列长度$N=256$,可以使用快速傅里叶变换算法高效地计算。
4.部分源码
`timescale 1ns / 1ps
module TEST();
reg i_clk;
reg i_rst;
reg start;
wire [15 : 0] m_axis_data_tdata;
dds_compiler_0 your_instance_name (
.aclk(i_clk), // input wire aclk
.aresetn(~i_rst), // input wire aresetn
.s_axis_config_tvalid(1'b1), // input wire s_axis_config_tvalid
.s_axis_config_tdata(32'd10000000), // input wire [31 : 0] s_axis_config_tdata
.m_axis_data_tvalid( ), // output wire m_axis_data_tvalid
.m_axis_data_tdata(m_axis_data_tdata), // output wire [15 : 0] m_axis_data_tdata
.m_axis_phase_tvalid(), // output wire m_axis_phase_tvalid
.m_axis_phase_tdata() // output wire [31 : 0] m_axis_phase_tdata
);
wire signed[7:0]Dreal = m_axis_data_tdata[15:8];
wire signed[7:0]Dimag = m_axis_data_tdata[7:0];
wire signed[27:0]o_fft_abs;
fft256 fft256_u(
.CLK (i_clk),
.RST (i_rst),
.ED (1'b1),
.START(start),
.SHIFT(4'b0000),
.DR ({Dreal[7],Dreal[7],Dreal[7],Dreal[7],Dreal[7],Dreal[7:3]}),
.DI (0),
.RDY (),
.OVF1 (),
.OVF2 (),
.ADDR (),
.o_fft_abs (o_fft_abs)
);
initial
begin
i_clk = 1'b1;
i_rst = 1'b1;
start = 1'b0;
#1000
i_rst = 1'b0;
start = 1'b1;
#10
start = 1'b0;
end
always #5 i_clk=~i_clk;
endmodule
00_028m
---





































