1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y52blZpr
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
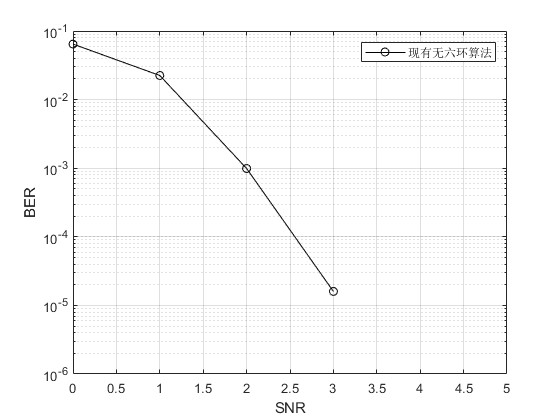
3.算法概述
近年来,ldpc码的优越性得到国内外科研工作者关注,并且已成为现代通信系统不可或缺的部分,被用来检测和修正由信道效应如噪声、衰减和干扰等引起的信息传输错误。然而,其性能提高的同时,编码复杂度也同样提高了,进而导致实际应用中成本增加和资源浪费。为了解决该问题,国内外学者提出了准循环低密度奇偶校验(quasi-cycliclow-densityparity-check,qc-ldpc)码,其校验矩阵由于具有准循环特性,因而在实际通信系统的应用中具有硬件容易实现的优点。
利用大衍数列的独特性质设计指数矩阵,并将其用来扩展原模图矩阵,得到的校验矩阵中不存在四环。因为原模图基矩阵由计算机搜索算法产生,具有列数可灵活改变的优点,并且该方案构造的校验矩阵中六环的数量相比于基于大衍数列构造法大大地减少了。基于大衍数列构造准循环低密度校验码的方法.该方法利用大衍数列固定项差对应的值单调递增的特点,构造出的校验矩阵不含有长度为4的环,具有准循环结构,节省了校验矩阵的存储空间.
4.部分源码
%%
%开始循环,进行误码率仿真
for i=1:length(SNR)
i
Bit_err(i) = 0; %设置误码率参数
Num_err = 0; %蒙特卡洛模拟次数
Numbers = 0; %误码率累加器
%信道参数
Hsd = 1;
Hsr = 1;
Hrd = 1;
while Num_err <= 100
fprintf('Eb/N0 = %f\n', SNR(i));
Num_err
N0 = 10^(-SNR(i)/10);
Trans_data = round(rand(N-M,1)); %产生需要发送的随机数
[ldpc_code,newH] = func_Enc(Trans_data,H1); %LDPC编码
u = [ldpc_code;Trans_data]; %LDPC编码
Trans_BPSK = 2*u-1; %BPSK
%S->D
Rec_sd = awgn(Trans_BPSK,SNR(i),'measured');
%接收端
[vhatsd,nb_itersd,successsd] = func_Dec(Rec_sd,newH,N0,Max_iter);
[nberr,rat] = biterr(vhatsd(M+1:N)',Trans_data);
%LDPC译码
Num_err = Num_err+nberr;
Numbers = Numbers+1;
end
Bit_err(i) = Num_err/(N*Numbers);
end
A166





































