1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWalZtw
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
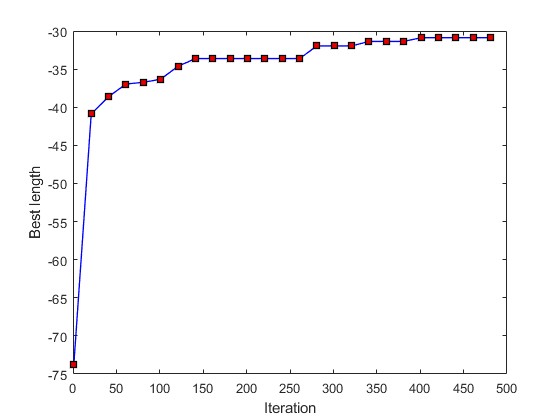
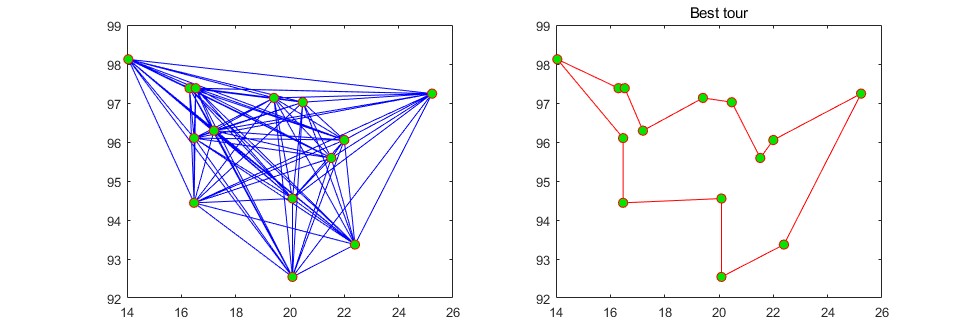
3.算法概述
模拟退火算法(simulated annealing,SAA)来源于固体退火原理,是一种基于概率的算法。模拟退火算法来源于固体退火原理,是一种基于概率的算法,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
模拟退火算法的搜索过程是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程,通过赋予搜索过程一种时变且最终趋于零的概率突跳性,从而可有效避免陷入局部极小并最终趋于全局最优的串行结构的优化算法。
以上特性使得模拟退火算法具备在路径规划领域应用的价值,比如用于解决旅行商问题(TSP)、有时间窗车辆路径问题(VRP)、有容量限制的VRP问题(CVRP)等.
模拟退火算法来源于固体退火原理,是一种基于概率的算法,将固体加温至充分高,再让其徐徐冷却,加温时,固体内部粒子随温升变为无序状,内能增大,而徐徐冷却时粒子渐趋有序,在每个温度都达到平衡态,最后在常温时达到基态,内能减为最小。
4.部分源码
.......................................................
graphNo = 1;
[ graph ] = createGraph(2);
nVar = graph.n;
A.position = randperm(nVar);
A.cost = fitnessFunction ( [A.position, A.position(1)] , graph);
figure
set(gcf,'position' , [50,50,700,700])
subplot(1,2,1)
drawGraph( graph);
% SA algorithm
T0=1;
T=T0;
alphaa=0.99;
maxIteration = 500;
bestFitness = inf;
bestTour = [];
fitness_hist = 0;
for t = 1 : maxIteration
fitness_hist(t) = A.cost;
B.position=createNeighbour(A.position);
B.cost = fitnessFunction ( [B.position, B.position(1)] , graph);
Delta = A.cost - B.cost;
if Delta < 0 % uphill move (good move)
A.cost = B.cost;
A.position = B.position;
else % downhill move (bad move)
P=exp(-Delta/T);
if rand<=P
A.cost = B.cost;
A.position = B.position;
end
end
T=alphaa*T;
outmsg = [ 'Iteration #' , num2str(t) , ' Shortest length = ' , num2str(A.cost) ];
disp(outmsg)
subplot(1,2,2)
title(['Iteration #' , num2str(t) ])
cla
drawBestTour( A.position, graph );
drawnow
end
figure
plot([1:20:maxIteration],fitness_hist(1:20:end),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
xlabel('Iteration')
ylabel('Best length')
A417





































