1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qWkp5q
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
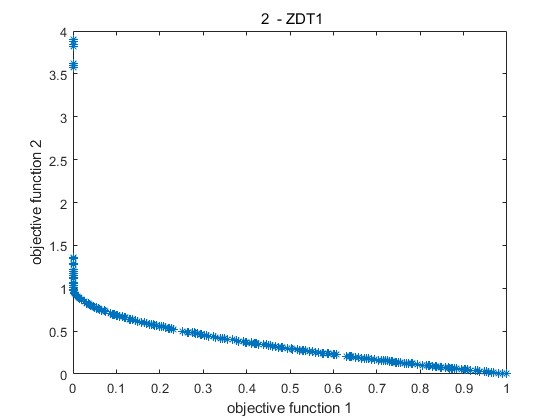
3.算法概述
将一群具有多个目标的个体(解集,或者说线代里的向量形式)作为父代初始种群,在每一次迭代中,GA操作后合并父代于自带。通过非支配排序,我们将所有个体分不到不同的pareto最优前沿层次。然后根据不同层次的顺序从pareto最优前沿选择个体作为下一个种群。出于遗传算法中的“物种多样性”保护,还计算量“拥挤距离”。拥挤距离比较将算法各阶段的选择过程引向一致的前沿。
4.部分源码
%% Description
%pop_size 染色体的数目
%gen_max 最大遗传代数
%gen_count 目前的迭代数
%M 目标函数的数量
%no_runs 运行次数
%xl,xu为设计变量的下限和上限
%最终的Pareto解在变量’parto_rank1’中,设计变量在coumns(1:V),目标函数在(V+1,V+M)
%约束在(V+M+1),排序在(V+M+2),拥挤距离在(V+M+3)中
%% code starts
M=2;
p=2;
pop_size=200; % Population size
no_runs=1; % Number of runs
gen_max=500; % MAx number of generations - stopping criteria
fname='test_case'; % Objective function and constraint evaluation
if p==13, % OSY
pop_size=100;
no_runs=10;
end;
if (p==2 | p==5 | p==7), gen_max=1000; end;
if p<=9 % Unconstrained test functions
tV=[2;30;3;1;30;4;30;10;10];
V=tV(p);
txl=[-5*ones(1,V);zeros(1,V);-5*ones(1,V);-1000*ones(1,V);zeros(1,V);-1/sqrt(V)*ones(1,V);zeros(1,V); 0 -5*ones(1,V-1);zeros(1,V)];
txu=[10*ones(1,V); ones(1,V);5*ones(1,V);1000*ones(1,V);ones(1,V);1/sqrt(V) *ones(1,V);ones(1,V);1 5*ones(1,V-1);ones(1,V)];
xl=(txl(p,1:V)); % lower bound vector
xu=(txu(p,1:V)); % upper bound vectorfor
etac = 20; % distribution index for crossover
etam = 20; % distribution index for mutation / mutation constant
else % Constrained test functions
p1=p-9;
tV=[2;2;2;6;2];
V=tV(p1);
txl=[0 0 0 0 0 0;-20 -20 0 0 0 0;0 0 0 0 0 0;0 0 1 0 1 0;0.1 0 0 0 0 0];
txu=[5 3 0 0 0 0;20 20 0 0 0 0;pi pi 0 0 0 0;10 10 5 6 5 10;1 5 0 0 0 0];
xl=(txl(p1,1:V)); % lower bound vector
xu=(txu(p1,1:V)); % upper bound vectorfor i=1:NN
etac = 20; % distribution index for crossover
etam = 100; % distribution index for mutation / mutation constant
end
pm=1/V; % Mutation Probability
Q=[];
for run = 1:no_runs
%% Initial population
xl_temp=repmat(xl, pop_size,1);
xu_temp=repmat(xu, pop_size,1);
x = xl_temp+((xu_temp-xl_temp).*rand(pop_size,V));
%% Evaluate objective function
for i =1:pop_size
[ff(i,:) err(i,:)] =feval(fname, x(i,:)); % Objective function evaulation
end
error_norm=normalisation(err); % Normalisation of the constraint violation
population_init=[x ff error_norm];
[population front]=NDS_CD_cons(population_init); % Non domination Sorting on initial population
%% Generation Starts
for gen_count=1:gen_max
% selection (Parent Pt of 'N' pop size)
parent_selected=tour_selection(population); % 10 Tournament selection
%% Reproduction (Offspring Qt of 'N' pop size)
child_offspring = genetic_operator(parent_selected(:,1:V)); % SBX crossover and polynomial mutation
for ii = 1:pop_size
[fff(ii,:) err(ii,:)]=feval(fname, child_offspring(ii,:)); % objective function evaluation for offspring
end
error_norm=normalisation(err);
child_offspring=[child_offspring fff error_norm];
%% INtermediate population (Rt= Pt U Qt of 2N size)
population_inter=[population(:,1:V+M+1) ; child_offspring(:,1:V+M+1)];
[population_inter_sorted front]=NDS_CD_cons(population_inter); % Non domination Sorting on offspring
%% Replacement - N
new_pop=replacement(population_inter_sorted, front);
population=new_pop;
end
new_pop=sortrows(new_pop,V+1);
paretoset(run).trial=new_pop(:,1:V+M+1);
Q = [Q; paretoset(run).trial]; % Combining Pareto solutions obtained in each run
end
A127





































