1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5mWlp1y
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
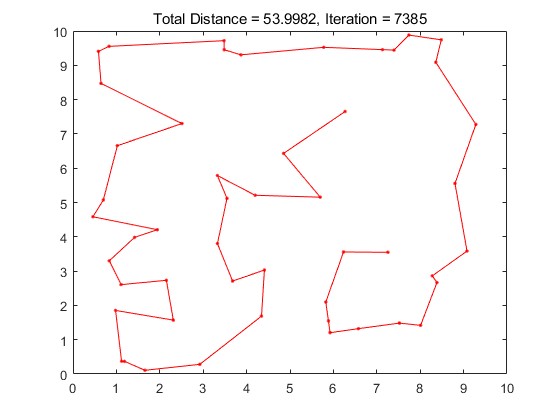
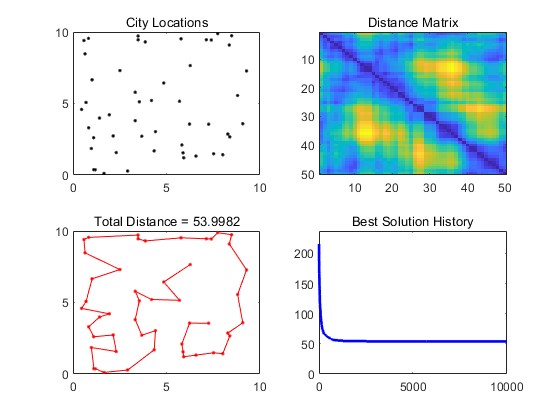
3.算法概述
旅行商问题,即TSP(Traveling Salesman Problem)是数学领域中著名问题之一。假设有一个旅行商人要拜访n个城市,他必须选择所要走的路径,路径的限制是每个城市只能拜访一次,而且最后要回到原来出发的城市。路径的选择目标是要求求得的路径路程为所有路径之中的最小值。TSP问题是一个组合优化问题,该问题可以被证明具有NPC计算复杂性。因此,任何能使该问题的求解得以简化的方法,都将受到高度的评价和关注。
遗传算法的基本思想正是基于模仿生物界遗传学的遗传过程。它把问题的参数用基因代表,把问题的解用染色体代表(在计算机里用二进制码表示),从而得到一个由具有不同染色体的个体组成的群体。这个群体在问题特定的环境里生存竞争,适者有最好的机会生存和产生后代。后代随机化地继承了父代的最好特征,并也在生存环境的控制支配下继续这一过程。群体的染色体都将逐渐适应环境,不断进化,最后收敛到一族最适应环境的类似个体,即得到问题最优的解。要求利用遗传算法求解TSP问题的最短路径。
4.部分源码
% Override default configuration with user inputs
configStruct = get_config(defaultConfig,userConfig);
% Extract configuration
xy = configStruct.xy;
dmat = configStruct.dmat;
popSize = configStruct.popSize;
numIter = configStruct.numIter;
showProg = configStruct.showProg;
showResult = configStruct.showResult;
showWaitbar = configStruct.showWaitbar;
if isempty(dmat)
nPoints = size(xy,1);
a = meshgrid(1:nPoints);
dmat = reshape(sqrt(sum((xy(a,:)-xy(a',:)).^2,2)),nPoints,nPoints);
end
% Verify Inputs
[N,dims] = size(xy);
[nr,nc] = size(dmat);
if N ~= nr || N ~= nc
error('Invalid XY or DMAT inputs!')
end
n = N;
% Sanity Checks
popSize = 4*ceil(popSize/4);
numIter = max(1,round(real(numIter(1))));
showProg = logical(showProg(1));
showResult = logical(showResult(1));
showWaitbar = logical(showWaitbar(1));
% Initialize the Population
pop = zeros(popSize,n);
pop(1,:) = (1:n);
for k = 2:popSize
pop(k,:) = randperm(n);
end
% Run the GA
globalMin = Inf;
totalDist = zeros(1,popSize);
distHistory = zeros(1,numIter);
tmpPop = zeros(4,n);
newPop = zeros(popSize,n);
if showProg
figure('Name','TSPO_GA | Current Best Solution','Numbertitle','off');
hAx = gca;
end
if showWaitbar
hWait = waitbar(0,'Searching for near-optimal solution ...');
end
for iter = 1:numIter
% Evaluate Each Population Member (Calculate Total Distance)
for p = 1:popSize
d = 0; % Open Path
for k = 2:n
d = d + dmat(pop(p,k-1),pop(p,k));
end
totalDist(p) = d;
end
% Find the Best Route in the Population
[minDist,index] = min(totalDist);
distHistory(iter) = minDist;
if minDist < globalMin
globalMin = minDist;
optRoute = pop(index,:);
if showProg
% Plot the Best Route
if dims > 2, plot3(hAx,xy(optRoute,1),xy(optRoute,2),xy(optRoute,3),'r.-');
else plot(hAx,xy(optRoute,1),xy(optRoute,2),'r.-'); end
title(hAx,sprintf('Total Distance = %1.4f, Iteration = %d',minDist,iter));
drawnow;
end
end
% Genetic Algorithm Operators
randomOrder = randperm(popSize);
for p = 4:4:popSize
rtes = pop(randomOrder(p-3:p),:);
dists = totalDist(randomOrder(p-3:p));
[ignore,idx] = min(dists); %#ok
bestOf4Route = rtes(idx,:);
routeInsertionPoints = sort(ceil(n*rand(1,2)));
I = routeInsertionPoints(1);
J = routeInsertionPoints(2);
for k = 1:4 % Mutate the Best to get Three New Routes
tmpPop(k,:) = bestOf4Route;
switch k
case 2 % Flip
tmpPop(k,I:J) = tmpPop(k,J:-1:I);
case 3 % Swap
tmpPop(k,[I J]) = tmpPop(k,[J I]);
case 4 % Slide
tmpPop(k,I:J) = tmpPop(k,[I+1:J I]);
otherwise % Do Nothing
end
end
newPop(p-3:p,:) = tmpPop;
end
pop = newPop;
% Update the waitbar
if showWaitbar && ~mod(iter,ceil(numIter/325))
waitbar(iter/numIter,hWait);
end
end
A104





































