1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5qWk5Zr
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
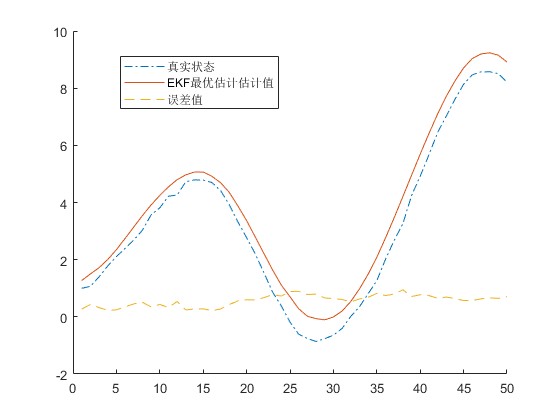
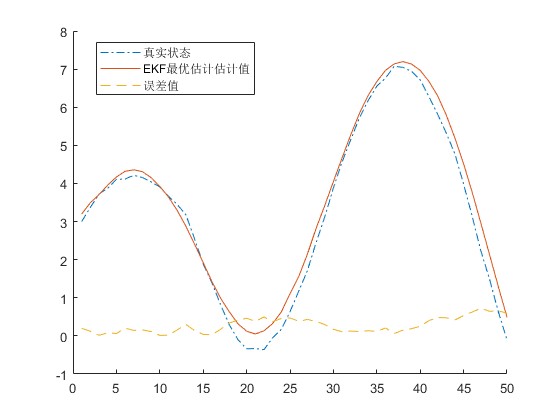
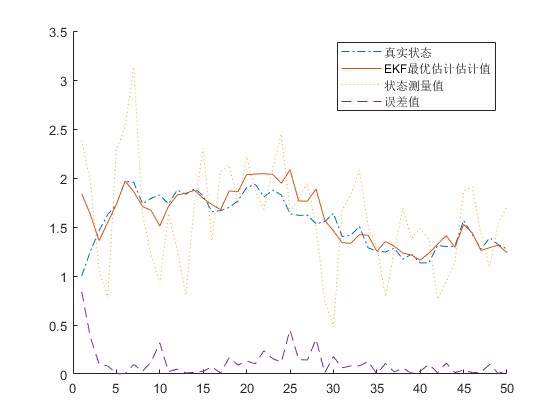
3.算法概述
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全包含噪声的测量中,估计动态系统的状态。这种滤波方法以它的发明者鲁道夫·E·卡尔曼(Rudolf E. Kalman)命名。卡尔曼最初提出的滤波理论只适用于线性系统。Bucy,Sunahara等人提出并研究了扩展卡尔曼滤波(EKF),将卡尔曼滤波理论进一步应用到非线性领域。扩展卡尔曼滤波(Extended Kalman Filter,EKF)是标准卡尔曼滤波在非线性情形下的一种扩展形式,EKF算法是将非线性函数进行泰勒展开,省略高阶项,保留展开项的一阶项,以此来实现非线性函数线性化,最后通过卡尔曼滤波算法近似计算系统的状态估计值和方差估计值,对信号进行滤波。
4.部分源码
%常系数
L= 0.3875; %单位(m)
Ix = 0.05887; %单位(kg·m^2)
Iy = 0.05887;
Iz = 0.13151;
g = 9.81; %单位(N/kg)
%动力学方程的常系数
a1 = -(Iy - Iz)/Ix;
a2 = -(Iz - Ix)/Iy;
a3 = -(Ix - Iy)/Iz;
b1 = L/Ix;
b2 = L/Iy;
b3 = 1/Iz;
Ts = 0.1; %采样时间
t = 5; %仿真时间
len = fix(t/Ts); %仿真步数
n = 6; %状态维度
w = 0.1; %过程标准差
v = 0.5; %测量标准差
Q = w^2*eye(n); %过程方差
R = v^2; %测量值的方差
h=@(x)[x(2);x(4);x(6)]; %测量方程
s=[1;2;3;3;2;1]; %初始状态
x=s+w*randn(6,1); %初始化状态
P = eye(6); %初始化协方差矩阵
xV = zeros(6,len); %EKF估计值
sV = zeros(6,len); %真实值
zV = zeros(3,len); %测量值
for k=1:len
%随机赋值控制量
u2 = 0.1*randn(1,1);
u3 = 0.1*randn(1,1);
u4 = 0.1*randn(1,1);
z = h(s) + v*randn;
sV(:,k)= s; %实际状态
zV(:,k) = z; %状态测量值
%状态方程
f=@(x)[x(1)+Ts*x(2);
(a1*x(4)*x(6) +b1*u2)*Ts+x(2);
x(3)+Ts*x(4);
(a2*x(2)*x(6) +b2*u3)*Ts+x(4);
x(5)+Ts*x(6);
(a3*x(2)*x(4) +b3*u4)*Ts+x(6);];
%一步预测,同时计算f的雅可比矩阵A
[x1,A]=jaccsd(f,x);
%过程方差预测
P=A*P*A'+Q;
%状态预测,同时计算h的雅可比矩阵H
[z1,H]=jaccsd(h,x1);
%计算卡尔曼增益
K=P*H'/(H*P*H'+R);
%状态EKF估计值
x=x1+K*(z-z1);
%协方差更新
P=P-K*H*P;
xV(:,k) = x;
%更新状态
s = f(s) + w*randn(6,1);
end
%俯仰角、滚转角、偏航角度值
for k=1:2:5
figure(); hold on;
plot(sV(k,:),'-.'); %画出真实值
plot(xV(k,:)) %画出最优估计值
plot(abs(sV(k,:)-xV(k,:)), '--'); %画出误差值
legend('真实状态', 'EKF最优估计估计值', '误差值');
end
A128





































