1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJaYlJds
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
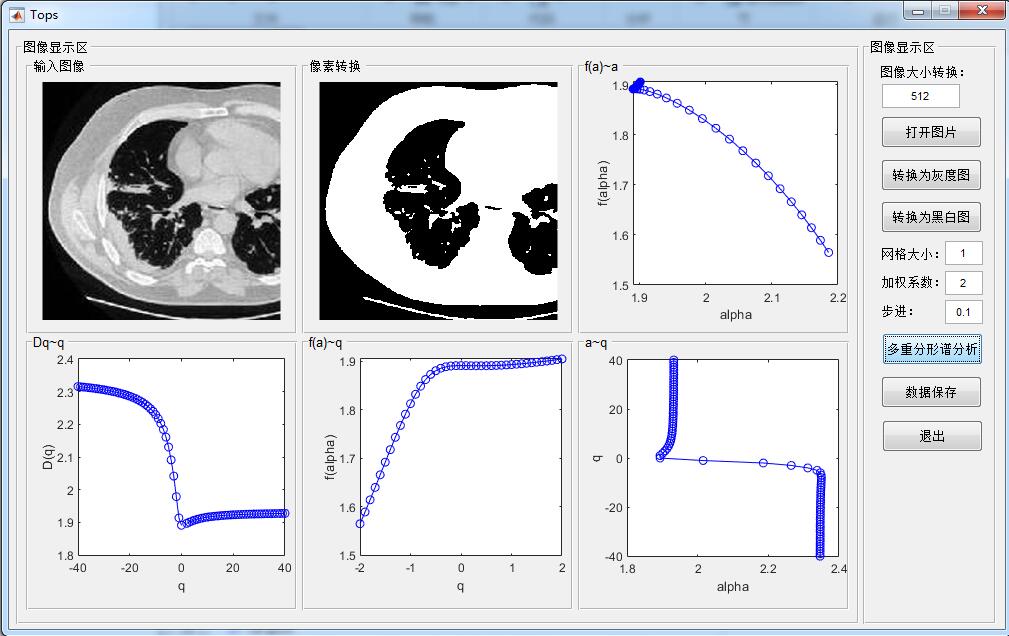
3.算法概述
多重分形(multifractal)一种分为多个区域的复杂分形结构。为了对分形的复杂性和不均匀性进行更细致地刻画,需引进它的概率分布函数及其各阶矩的计算,由此构成了分形维数的一个连续谱,称之为多重分形或多标度分形。
4.部分源码
...............................................................................
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Qran = 20*qs;
for kj=1:p
count = 0;
No_boxes = power(Rs,2)/power(power(2,kj),2);
for q = -Qran:10*qstep:Qran
qsum = 0;
for i=1:No_boxes
if PsL(i,kj) ~= 0
qsum = qsum + power(PsL(i,kj),q);
end
end
fqnum = 0;
aqnum = 0;
smuiqL = 0;
for i=1:No_boxes
if PsL(i,kj) ~= 0
muiqL = power(PsL(i,kj),q)/qsum;
fqnum = fqnum + (muiqL * log(muiqL));
aqnum = aqnum + (muiqL * log(PsL(i,kj)));
smuiqL = smuiqL + muiqL;
end
end
count = count + 1;
fql(kj,count) = fqnum;
aql(kj,count) = aqnum;
qval(count) = q;
end
end
for i=1:count
line = polyfit(logl,aql(:,i),1);
aq(i) = line(1);
yfit = polyval(line,logl);
sse = sum(power(aql(:,i)-yfit,2));
sst = sum(power(aql(:,i)-mean(aql(:,i)),2));
ar2(i) = 1-(sse/sst);
end
for i=1:count
line = polyfit(logl,fql(:,i),1);
fq(i) = line(1);
yfit = polyval(line,logl);
sse = sum(power(fql(:,i)-yfit,2));
sst = sum(power(fql(:,i)-mean(fql(:,i)),2));
fr2(i) = 1-(sse/sst);
end
for i=1:count
Dq(i) = (aq(i)*qval(i)-fq(i))/(qval(i)-1);
end
aqs = aq;
fqs = fq;
qvals = qval;
Dqs = Dq;
09_034_m





































