1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJWbmpZx
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
3.算法概述
LDPC ( Low-density Parity-check,低密度奇偶校验)码是由 Gallager 在1963 年提出的一类具有稀疏校验矩阵的线性分组码 (linear block codes),然而在接下来的 30 年来由于计算能力的不足,它一直被人们忽视。1996年,D MacKay、M Neal 等人对它重新进行了研究,发现 LDPC 码具有逼近香农极限的优异性能。并且具有译码复杂度低、可并行译码以及译码错误的可检测性等特点,从而成为了信道编码理论新的研究热点。
1.译码器是基于归一化最小和算法
2.码型选择:CCSDS标准中推荐的用于深空通信的(8176,7154)QC-LDPC码,码率为7/8(0.875)
3.(8176,7154)QC-LDPC码的校验矩阵程序(Matlab)
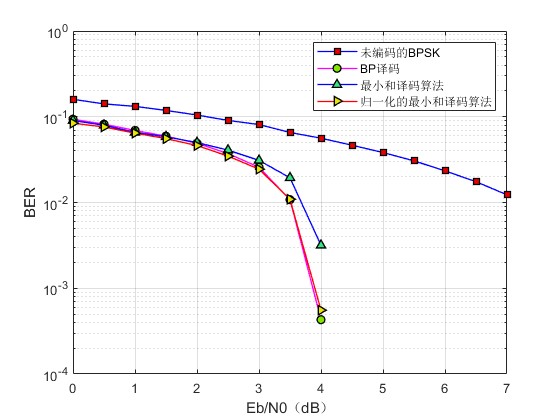
4.BP译码算法,最小和译码算法(MSA),归一化的最小和译码算法以及未经编码的采用BPSK调制。这几种译码算法的误码率对比程序及误码率曲线对比图。
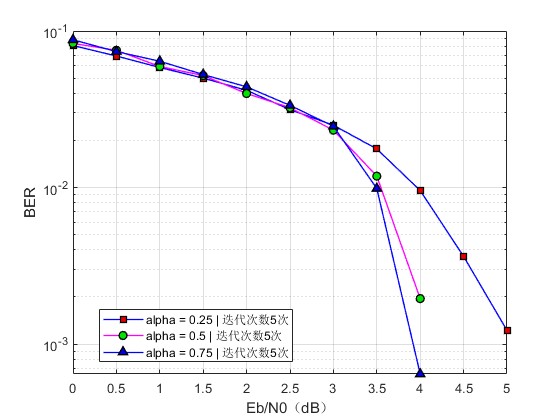
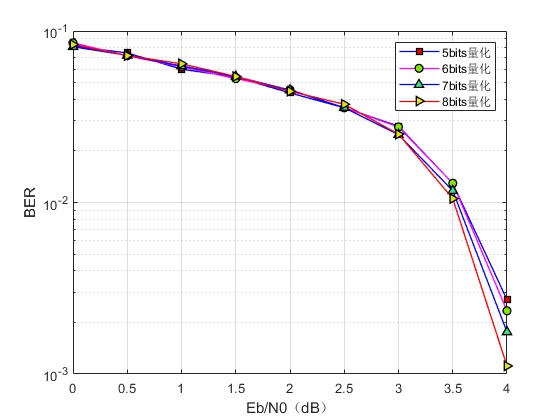
5.归一化最小和译码算法中修正因子α的选取,考虑选取在不同迭代次数下的α的平均值,给出选取过程的文档,再在取定的α下仿真比较最小和译码算法和归一化最小和译码算法在不同迭代次数下的误码率(matlab)
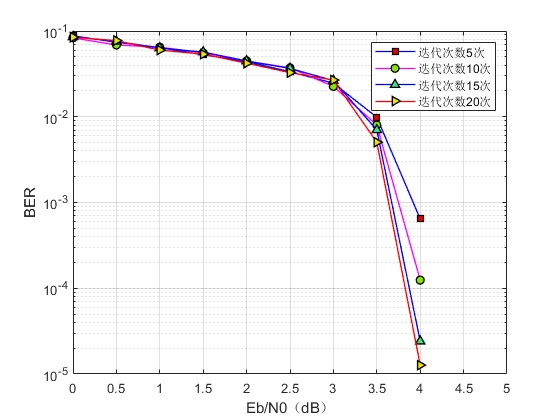
6.采用归一化最小和译码算法在不同迭代次数的仿真程序以及对比图,作为选择最大迭代次数的依据(matlab)
4.部分源码
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。
% rx: 接收到序列
% H: 校验矩阵
% iteration: 译码迭代次数
% parameter: 归一化参数,值为1表最小和算法;值为其他值,是对最小和算法的改进,归一化最小和,参数一般为常数0.75
[M N] = size(H);
Lci = rx;
Lrji = zeros(M, N);
Pibetaij = zeros(M, N);
Lqij = H.*repmat(Lci, M, 1);
for n = 1:iteration
n
alphaij = sign(Lqij);
betaij = abs(Lqij);
% ----- Horizontal step -----
for i = 1:M
c1 = find(H(i, :));
for k = 1:length(c1)
minOfbetaij = realmax;
for l = 1:length(c1)
if l ~= k
if betaij(i, c1(l)) < minOfbetaij
minOfbetaij = betaij(i, c1(l));
end
end
end
prodOfalphaij = prod(alphaij(i, c1))*alphaij(i, c1(k)); %找到出去当前位的符合乘积
Lrji(i, c1(k)) =parameter*prodOfalphaij*minOfbetaij;
end
end
% ------ Vertical step ------
for j = 1:N
r1 = find(H(:, j));
for k = 1:length(r1)
Lqij(r1(k), j) = Lci(j) + sum(Lrji(r1, j)) - Lrji(r1(k), j);
end
LQi = Lci(j) + sum(Lrji(r1, j));
if LQi < 0
vHat(j) = 1;
else
vHat(j) = 0;
end
end
if H*vHat'==zeros(M,1)
break;
end
end
% fprintf('Min-sum is done...\n');
14_022_m





































