1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y5mamZpt
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
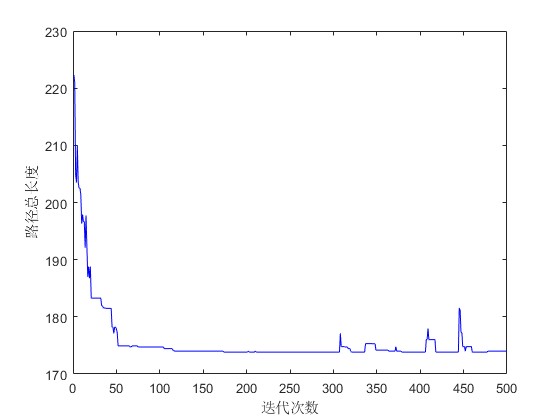
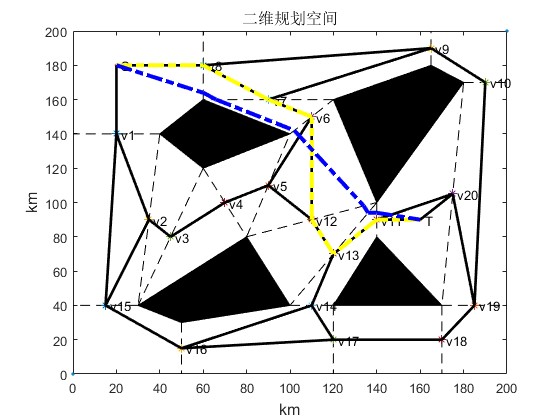
3.算法概述
蚁群系统(Ant System或Ant Colony System)是由意大利学者Dorigo、Maniezzo等人于20世纪90年代首先提出来的。他们在研究蚂蚁觅食的过程中,发现单个蚂蚁的行为比较简单,但是蚁群整体却可以体现一些智能的行为。例如蚁群可以在不同的环境下,寻找最短到达食物源的路径。这是因为蚁群内的蚂蚁可以通过某种信息机制实现信息的传递。后又经进一步研究发现,蚂蚁会在其经过的路径上释放一种可以称之为“信息素”的物质,蚁群内的蚂蚁对“信息素”具有感知能力,它们会沿着“信息素”浓度较高路径行走,而每只路过的蚂蚁都会在路上留下“信息素”,这就形成一种类似正反馈的机制,这样经过一段时间后,整个蚁群就会沿着最短路径到达食物源了。
4.部分源码
....................
%% 障碍物数据
position = load('barrier.txt');
plot([0,200],[0,200],'.');
hold on
B = load('barrier.txt');
xlabel('km','fontsize',12)
ylabel('km','fontsize',12)
title('二维规划空间','fontsize',12)
%% 描述起点和终点
S = [20,180];
T = [160,90];
plot([S(1),T(1)],[S(2),T(2)],'.');
% 图形标注
text(S(1)+2,S(2),'S');
text(T(1)+2,T(2),'T');
%% 描绘障碍物图形
fill(position(1:4,1),position(1:4,2),[0,0,0]);
fill(position(5:8,1),position(5:8,2),[0,0,0]);
fill(position(9:12,1),position(9:12,2),[0,0,0]);
fill(position(13:15,1),position(13:15,2),[0,0,0]);
% 下载链路端点数据
L = load('lines.txt');
%% 描绘线及中点
v = zeros(size(L));
for i=1:20
plot([position(L(i,1),1),position(L(i,2),1)],[position(L(i,1),2)...
,position(L(i,2),2)],'color','black','LineStyle','--');
v(i,:) = (position(L(i,1),:)+position(L(i,2),:))/2;
plot(v(i,1),v(i,2),'*');
text(v(i,1)+2,v(i,2),strcat('v',num2str(i)));
end
%% 描绘可行路径
sign = load('matrix.txt');
[n,m]=size(sign);
for i=1:n
if i == 1
for k=1:m-1
if sign(i,k) == 1
plot([S(1),v(k-1,1)],[S(2),v(k-1,2)],'color',...
'black','Linewidth',2,'LineStyle','-');
end
end
continue;
end
for j=2:i
if i == m
if sign(i,j) == 1
plot([T(1),v(j-1,1)],[T(2),v(j-1,2)],'color',...
'black','Linewidth',2,'LineStyle','-');
end
else
if sign(i,j) == 1
plot([v(i-1,1),v(j-1,1)],[v(i-1,2),v(j-1,2)],...
'color','black','Linewidth',2,'LineStyle','-');
end
end
end
end
path = DijkstraPlan(position,sign);
j = path(22);
plot([T(1),v(j-1,1)],[T(2),v(j-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');
i = path(22);
j = path(i);
count = 0;
while true
plot([v(i-1,1),v(j-1,1)],[v(i-1,2),v(j-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');
count = count + 1;
i = j;
j = path(i);
if i == 1 || j==1
break;
end
end
plot([S(1),v(i-1,1)],[S(2),v(i-1,2)],'color','yellow','LineWidth',3,'LineStyle','-.');
count = count+3;
pathtemp(count) = 22;
j = 22;
for i=2:count
pathtemp(count-i+1) = path(j);
j = path(j);
end
path = pathtemp;
% path = [1 9 8 7 13 14 12 22];
%% 蚁群算法参数初始化
pathCount = length(path)-2; %经过线段数量
pheCacuPara=2; %信息素计算参数
pheThres = 0.8; %信息素选择阈值
pheUpPara=[0.1 0.0003]; %信息素更新参数
qfz= zeros(pathCount,10); %启发值
phePara = ones(pathCount,10)*pheUpPara(2); %信息素
qfzPara1 = ones(10,1)*0.5; %启发信息参数
qfzPara2 = 1.1; %启发信息参数
m=10; %种群数量
NC=500; %循环次数
pathk = zeros(pathCount,m); %搜索结果记录
shortestpath = zeros(1,NC); %进化过程记录
%% 初始最短路径
dijpathlen = 0;
vv = zeros(22,2);
vv(1,:) = S;
vv(22,:) = T;
vv(2:21,:) = v;
for i=1:pathCount-1
dijpathlen = dijpathlen + sqrt((vv(path(i),1)-vv(path(i+1),1))^2+(vv(path(i),2)-vv(path(i+1),2))^2);
end
LL = dijpathlen;
%% 经过的链接线
lines = zeros(pathCount,4);
for i = 1:pathCount
lines(i,1:2) = B(L(path(i+1)-1,1),:);
lines(i,3:4) = B(L(path(i+1)-1,2),:);
end
bestPath=zeros(pathCount,1);
%% 循环搜索
for num = 1:NC
%% 蚂蚁迭代寻优一次
for i=1:pathCount
for k=1:m
q = rand();
qfz(i,:) = (qfzPara2-abs((1:10)'/10-qfzPara1))/qfzPara2; %启发信息
if q<=pheThres%选择信息素最大值
arg = phePara(i,:).*(qfz(i,:).^pheCacuPara);
j = find(arg == max(arg));
pathk(i,k) = j(1);
else % 轮盘赌选择
arg = phePara(i,:).*(qfz(i,:).^pheCacuPara);
sumarg = sum(arg);
qq = (q-pheThres)/(1-pheThres);
qtemp = 0;
j = 1;
while qtemp < qq
qtemp = qtemp + (phePara(i,j)*(qfz(i,j)^pheCacuPara))/sumarg;
j=j+1;
end
j=j-1;
pathk(i,k) = j(1);
end
% 信息素更新
phePara(i,j) = (1-pheUpPara(1))*phePara(i,j)+pheUpPara(1)*pheUpPara(2);
end
end
%% 计算路径长度
len = zeros(1,k);
for k=1:m
Pstart = S;
Pend = lines(1,1:2) + (lines(1,3:4)-lines(1,1:2))*pathk(1,k)/10;
for l=1:pathCount
len(1,k) = len(1,k)+sqrt(sum((Pend-Pstart).^2));
Pstart = Pend;
if l<pathCount
Pend = lines(l+1,1:2) + (lines(l+1,3:4)-lines(l+1,1:2))*pathk(l+1,k)/10;
end
end
Pend = T;
len(1,k) = len(1,k)+sqrt(sum((Pend-Pstart).^2));
end
%% 更新信息素
% 寻找最短路径
minlen = min(len);
minlen = minlen(1);
minant = find(len == minlen);
minant = minant(1);
% 更新全局最短路径
if minlen < LL
LL = minlen;
bestPath=pathk(:,minant);
end
% 更新信息素
for i=1:pathCount
phePara(i,pathk(i,minant)) = (1-pheUpPara(1))* phePara(i,pathk(i,minant))+pheUpPara(1)*(1/minlen);
end
shortestpath(num) = minlen;
end
A109





































