1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/ZJaXmZlv
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
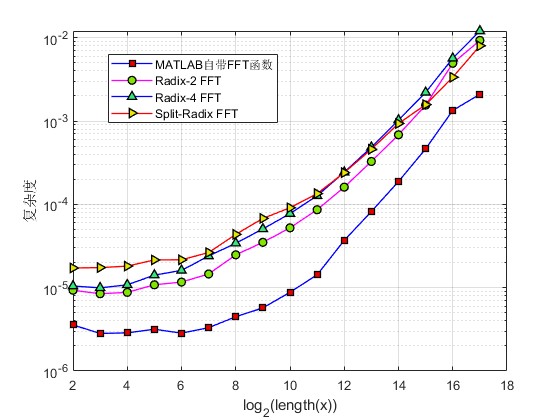
3.算法概述
FFT的基本思想是把原始的N点序列,依次分解成一系列的短序列。充分利用DFT计算式中指数因子 所具有的对称性质和周期性质,进而求出这些短序列相应的DFT并进行适当组合,达到删除重复计算,减少乘法运算和简化结构的目的。此后,在这思想基础上又开发了高基和分裂基等快速算法,随着数字技术的高速发展,1976年出现建立在数论和多项式理论基础上的维诺格勒傅里叶变换算法(WFTA)和素因子傅里叶变换算法。它们的共同特点是,当N是素数时,可以将DFT算转化为求循环卷积,从而更进一步减少乘法次数,提高速度。
4.部分源码
...........................................................
N = 2.^(2:1:17);
L = length(N);
TIMES = zeros(4,L);
for k = 1:L
for ij = 1:2000
[k,ij]
a = randn(1,N(k)) + 1i*randn(1,N(k));
tic
A1 = fft(a);
TIMES(1,k,ij) = toc;
tic
A2 = radix2fft(a);
TIMES(2,k,ij) = toc;
tic
A3 = radix4fft(a);
TIMES(3,k,ij) = toc;
tic
A4 = splitradixfft(a);
TIMES(4,k,ij) = toc;
end
end
figure;
semilogy(log2(N),mean(TIMES(1,:,:),3),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on;
semilogy(log2(N),mean(TIMES(2,:,:),3),'-mo',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.5,0.9,0.0]);
hold on;
semilogy(log2(N),mean(TIMES(3,:,:),3),'-b^',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.2,0.9,0.5]);
hold on;
semilogy(log2(N),mean(TIMES(4,:,:),3),'-r>',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.9,0.0]);
grid on;
legend('MATLAB自带FFT函数','Radix-2 FFT','Radix-4 FFT','Split-Radix FFT');
xlabel('log_2(length(x))');
ylabel('复杂度');
A548





































