1.完整项目描述和程序获取
>面包多安全交易平台:https://mbd.pub/o/bread/Y56Tmpxq
>如果链接失效,可以直接打开本站店铺搜索相关店铺:
>如果链接失效,程序调试报错或者项目合作也可以加微信或者QQ联系。
2.部分仿真图预览
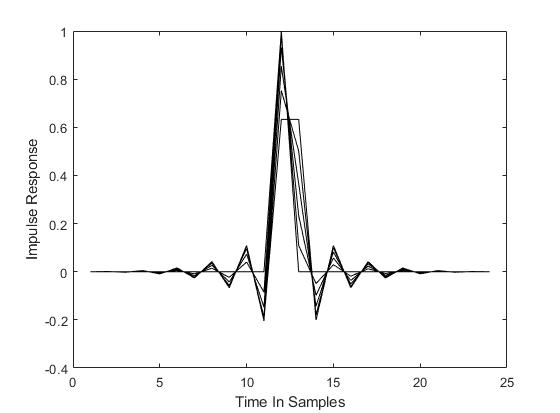
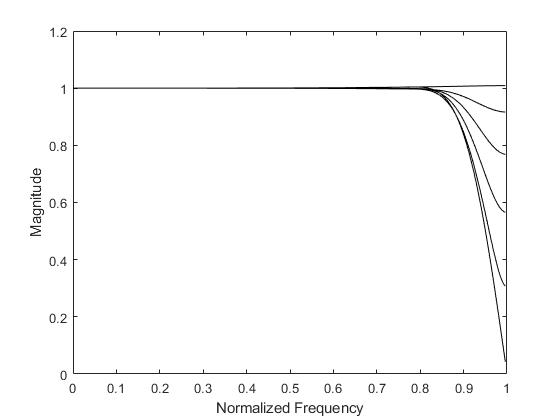
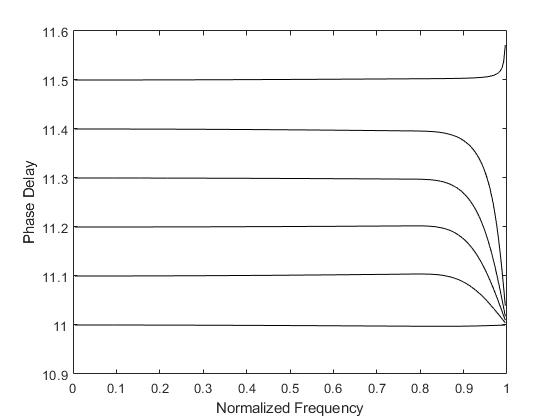
3.算法概述
farrow滤波器是一种连续可变时延的分数时延滤波器,这种滤波器的结构是由farrowcw于1988年提出,起初是用来解决声纳学中的分数时延问题。普通数字延时滤波器虽然结构简单,但系数计算过程复杂,在延时参数快速变化时,系数更新速度无法满足实时性要求,在工程应用上受限制。采用farrow结构数字延时滤波器能够更加灵活高效地进行分数延时滤波,延时参数改变时,无需重新计算滤波器系数,更容易在现场可编程门阵(fpga)上实现。信号处理的fpga实现过程中,往往需要大量消耗的乘法资源,从而导致fpga的乘法器资源成为系统瓶颈,本设计介绍了一种基于fpga的farrow滤波器设计方法,该方法采用对称结构的滤波器求解方法,充分利用乘法资源,高效实现farrow滤波器功能。
4.部分源码
N = 23; % filter order, odd better
L = N+1; % filter length;
Npt = 256; % no. of frequency points for plots
w = (0:1:Npt-1)/Npt; % frequenc scan (0,1)
delay = [0 0.1 0.2 0.3 0.4 0.5]; % delay range x=0..0.5
Nfil = length(delay); % number of filters
h = zeros(1,L); % impulse response vector
hvec=zeros(Nfil,L); % impulse response coefficient matrix
magresp = zeros(Nfil,Npt);
phasdel = zeros(Nfil,Npt-1);
xvec=zeros(Nfil,1); % fractional delay vector
P = 2; % polynomial order for FARROW structure (ca. 1-5)
C=zeros(P+1,N+1); % polynomial coeff. matrix
wp = 0.8; % normalized bandwidth (0-1.0)
for i=1:Nfil
...............................................................
end
for k=1:N+1
cc=polyfit(xvec,hvec(:,k),P); % fit P:th-order polynomial to each coeff set
C(:,k)=cc';
end
for j=1:Nfil
d=delay(j);
if d==0
d=d+0.0000001; % add 0.001 to avoid sin(0)/0;
end
h = C(P+1,:); % coeffs. via pol. approximation
for n=1:P
h=h+d^n*C(P+1-n,:);
end
h=h/sum(h); % scale response at zero freq. to unity
H = freqz(h,1,w*pi);
magresp(j,:) = abs(H);
uwphase=-unwrap(angle(H));
phasdel(j,:) = uwphase(2:Npt)./(w(2:Npt).*pi); % avoid divide by zero
end
A196





































